Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 9.Problemas - Ex. 60
Um estudante de graduação está processando seu código de para seu projeto de pesquisa de mestrado e gera um gráfico das linhas de corrente de um escoamento (contornos de função corrente constante). Os contornos são formados por valores igualmente espaçados da função corrente. A professora olha para o gráfico e imediatamente aponta para uma região de escoamento e diz: “Veja como o escoamento está rápido aqui!”. O que a professora notou sobre as linhas de corrente naquela região e como ela sabia que o escoamento era rápido naquela região?
Passo 1
Iremos discutir como uma pessoa interpreta a velocidade relativa em um gráfico de contorno de funções de corrente.
Assumindo que o fluxo é constante, incompressível e uma função de um plano .
Temos a seguinte situação:
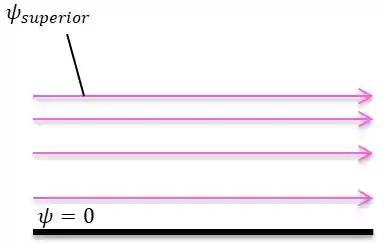
Para uma função de corrente que opera um plano e é incompressível a diferença de valores entre uma linha de fluxo de corrente é igual ao fluxo volumétrico por unidade de largura entre às duas linhas de fluxo.
Portanto, Quão mais próximas às linhas estiverem uma da outra, teremos uma velocidade relativa maior, e quanto mais separadas o resultado será uma velocidade relativa menor.
Passo 2
Seguindo oque foi dito no passo 1.
Por exemplo, . É positivo e representa o fluxo volumétrico por unidade de largura entre as linhas, entre parede a linha superior.
Logo, oque a professora observou foi a parte superior da nossa situação. Em que, a região, que possui linhas de fluxo bem próximas, implica uma alta velocidade relativa na região do fluxo.
Resposta
Linhas próximas implica uma alta velocidade relativa na região do fluxo.