Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 9.Problemas - Ex. 61

São mostrados linhas de emissão na Figura para escoamento de água sobre a parte dianteira de um cilindro rombudo, axissimétrico alinhado com o escoamento. As linhas de emissão são geradas introduzindo-se bolhas de ar em pontos igualmente espaçados a montante de campo de visão. É mostrada somente a metade superior, pois o escoamento é axissimétrico em relação ao eixo horizontal. Como o escoamento é permanente, as linhas de emissão são coincidentes com as linhas de corrente. Discuta como você pode dizer com base em um padrão de linha de corrente se a velocidade de escoamento em uma região em particular do campo de escoamento é (relativamente) grande ou pequena.

Passo 1

Para as linhas de escoamento dadas, temos que discutir como afirmar sobre a velocidade relativa com base na imagem do fluido.

Assumindo que o fluxo é constante, incompressível e aximétrico.

Aximétrico é estranho né, significa que o fluxo opera apenas no plano .

Para uma função de corrente que opera um plano e é incompressível a diferença de valores entre uma linha de fluxo de corrente é igual ao fluxo volumétrico por unidade de largura entre às duas linhas de fluxo.

Portanto, Quão mais próximas às linhas estiverem uma da outra, teremos uma velocidade relativa maior, e quanto mais separadas o resultado será uma velocidade relativa menor.

Passo 2

Seguindo oque foi dito no passo 1, temos:

Considerando que quão mais branco maior a quantidade de linhas de fluxo, nestas duas regiões que destaquei em laranja:

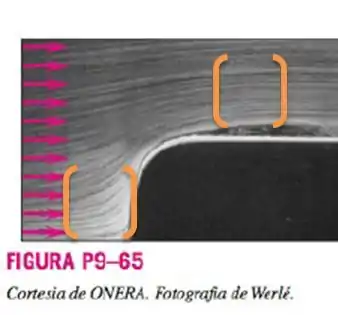
Possuímos uma velocidade relativa grande.

Passo 3

Considerando que quão mais escuro menor a quantidade de linhas de fluxo, temos nesta região em vermelho:

Possuímos uma velocidade relativa pequena.

Está região em específico é chamado de bolha de separação, caso você desejar entender oque acontece nesta bolha à questão 9-59 é uma boa pedida.

Resposta

Linhas de fluxo muito próximas temos uma alta velocidade relativa, linhas de fluxo bem separadas uma velocidade relativa bem baixa, como na bolha da separação.

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um escoamento permanente, bidimensional, tem o seguinte potencial de velocidade em coordenadas polares: ϕ = C r c o s θ + K l n r em que C e K são constantes. Determine a função correnteψ ( r ,θ ) par

Em coordenadas esféricas polares, como na Figura P4.12, o escoamento é chamado de escoamento com simetria axial se v θ ≡ 0e∂ ∂ θ ≡ 0 , de forma que v r = v r r ,θev θ = v θ r , θ . Mostre que para ess

Um modelo CFD do escoamento incompressível permanente bidimensional imprimiu os valores da função corrente ψ (x, y), em m²/s, em cada um dos quatro cantos de uma pequena célula de 10 cm por 10 cm, com

Para a distribuição de velocidade do Problema P4.4, determine se existe uma função corrente e, se existir, encontre uma expressão para ψ ( x , y ) e faça o esboço da linha de corrente que passa pelo p

O veleiro a rotor Flettner na figura E8.2 tem um coeficiente de arrasto na água de 0,006 baseado na área molhada de 4,18 m². Se o rotor gira a 200 rpm, encontre a máxima velocidade do barco que pode s