Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 4.Problemas - Ex. 73

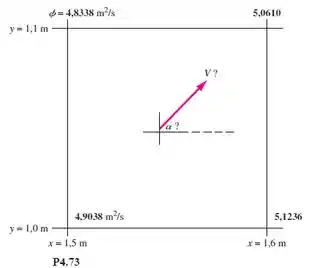
Um modelo CFD do escoamento incompressível permanente bidimensional imprimiu os valores da função potencial de velocidade (x, y), em m²/s, em cada um dos quatro cantos de uma pequena célula de 10 cm por 10 cm, como mostra a Figura P4.73. Use esses números

para calcular a velocidade resultante no centro da célula e seu ângulo α com relação ao eixo x.

Passo 1

Bora pra mais uma!

Note que os valores de são menores à esquerda do que à direita, o que indica que tem sentido apontado para a direita. Da mesma forma, são maiores na parte inferior, o que indica que tem sentido positivo para baixo. Para calcular a velocidade resultante no centro da célula, vamos definir os valores médios em cada lateral:

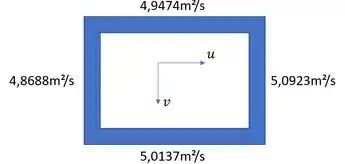
Então:

Para calcular a velocidade escalar tiraremos o modulo do vetor velocidade, assim a velocidade no centro da célula será:

E o ângulo formado com o eixo x é dado por:

Note que o vetor velocidade tem o sentido apontado para direita e para baixo, logo este ângulo representa -18,36

Resposta

A velocidade resultante no centro da célula tem valor de 2,331m/s, aponta para a direita e para baixo, formando um ângulo de 18,36 em relação ao eixo x.

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

13 – Um pequeno tanque de peixes é aproximado por um formato de semicorpo, como mostra a Fig. 8.13. O ponto O, a 0,5 m de distância da borda esquerda do tanque, é uma fonte de água descarregando aprox

59 – Considere o escoamento não viscoso em torno de um cilindro com circulação nula, como na Fig. 8.14a (mostrada abaixo). Encontre (a) o ponto sobre a superfície frontal onde a aceleração do fluido a

PP8.3 – Considere água a 20°C escoando a 12 m/s em um canal. Um oval de Rankine cilíndrica de 40 cm de comprimento é posicionada paralelamente ao escoamento, onde a pressão estática da água é 120 kPa.

PP8.2 – Modifique o Problema PP8.1 para determinar a distribuição de fontes pontuais que aproxima um corpo de revolução de formato “0018”. Uma vez que não existe resultados publicados, simplesmente se

An incompressible, irrotational, two-dimensional fl ow hasthe following stream function in polar coordinates:ψ 5 A rn sin (nθ) where A and n are constants.Find an expression for the velocity potential