Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 6.Problemas - Ex. 57
Em uma experiência de laboratório, água escoa radialmente para fora através do espaço entre dois discos planos paralelos, com velocidade moderada. O perímetro dos discos é aberto para a atmosfera. Os discos têm diâmetro e o espaçamento entre eles é . A vazão mássica medida da água é . Estime a pressão estática teórica no espaço entre os discos em , considerando escoamento sem atrito. Na situação de laboratório, em que algum atrito existe, a pressão medida nesse local nos discos seria acima ou abaixo do valor teórico? Por quê?
Passo 1
Vamos começar ilustrando o problema descrito no enunciado:
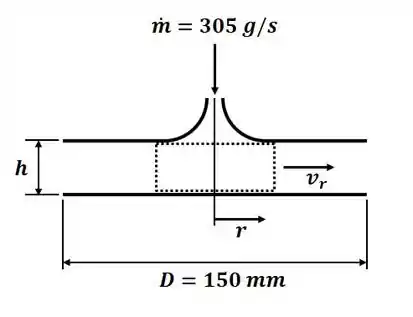
Agora vamos aplicar o princípio da continuidade para o sistema, pois toda a vazão mássica que entra por cima deve sair radialmente, então temos:
Nesse caso, a área seria a circunferência dos discos multiplicada pela altura entre eles, então temos:
Então, isolando da equação:
Então agora podemos calcular a velocidade para :
Agora vamos calcular a velocidade na extremidade dos discos em :
Passo 2
Agora podemos aplicar a equação de Bernoulli entre o ponto (1) e a extremidade do disco (2)
Como a extremidade do disco está exposta ao ambiente, temos , nesse caso, vamos encontrar uma pressão manométrica, sabemos também que a diferença entre as cotas e pode ser desprezada, então, substituindo os valores conhecidos:
Passo 3
Numa situação real, onde teríamos forças de atrito, então essas forças causariam uma queda de pressão conforme o escoamento avaça na direção de ilustrado no passo 1. Então, como a pressão na saída deve permanecer como sendo a pressão atmosférica, para atender a esse quesito, a pressão no ponto medido seria maior do que a teórica encontrada no passo 2.