Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 7.Problemas - Ex. 79
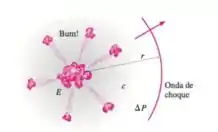
Uma explosão ocorre na atmosfera quando um míssil antiaéreo se choca com seu alvo (Figura ). Uma onda de choque (também chamada de onda de explosão) se espalha radialmente a partir da explosão. A diferença de pressão através da onda de explosão e sua distância radial do centro são funções do tempo , da velocidade do som e da quantidade total de energia liberada pela explosão.
(a) Gere relações adimensionais entre e os outros parâmetros e entre e os outros parâmetros.
(b) Para determinada explosão, se o tempo desde a explosão dobrar, com todas as outras condições iguais, por qual fator diminuirá?
Passo 1
Vamos lá, para o item (a) o primeiro passo consiste em listar os parâmetros. Existem parâmetros nesse problema, são eles:
No segundo passo, temos as seguintes dimensões primárias dos parâmetros:
No terceiro passo, como primeira tentantiva tomamos que corresponde a quantidade de dimensões primárias do problema . Se este valor de , estiver certo, o numero de esperado é
No quarto passo, nós precisamos escolher parametros repetidos. Nesse caso temos todos os parâmetros como independentes.
No quinto passo, geramos o dependente :
Calculando os expoentes para cada dimensão:
Massa:
Tempo:
Comprimento:
Substituindo no :
Como não é estabelecido, no sexto passo, deixamos assim e escrevemos como constante:
Passo 2
Ainda no item (a) para relacionar o com os outros parâmetros, não temos muitos cálculos para fazer, uma vez que a distância é dada através de medições.
Relacionando com as variáveis repetidas, temos:
Como não temos outro , deixamos assim e escrevemos como constante:
Passo 3
Para o item (b), dobrando o tempo, usando a equação que encontramos, temos:
Ou seja, diminuirá a um fator .
Prontinho!!
Resposta
(a) e ;
(b) .