Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 8.Problemas - Ex. 67
Um dos extremos de um tubo horizontal é conectado por meio de cola a um tanque pressurizado contendo líquido, e o outro extremo possui uma tampa. O diâmetro interno do tubo é 2,5 cm, e a pressão no tanque é 250 kPa(manométrica). Determine a força que a cola deve resistir com o tubo tampado, e a força que a cola deve resistir quando a tampa é retirada, com o líquido sendo descarregado para a atmosfera.
Passo 1
Neste problema é pedido a força que uma cola que conecta um tubo a um tanque irá resistir na situação de tubo fechado e aberto.
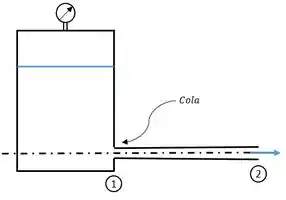
Para isso será necessário o uso da equação de Balanço de Quantidade de Movimento (relação integral) ao longo de um volume de controle, conforme Figura abaixo.
A equação de Balanço de Quantidade de Movimento, aplicada apenas ao longo de x, é definida como:
E será aplicada ao longo das seções 1 e 2, tendo como hipóteses:
- regime permanente ();
- escoamento incompressível ();
- escoamento completamente desenvolvido (
- seção transversal constante (;
- escoamento horizontal (força de campo nula - );
- (manométrica);
- (pressão atmosférica em termos manométrico);
- ;
- escoamento horizontal (força de campo nula - ).
Passo 2
- Considerando tubo fechado
Por meio de uma balanço de forças é possível definir a força que a cola irá resistir como:
Ou seja, na situação de fluido parado a cola deverá resistir à pressão exercida pelo fluido, qual é dada por:
Utilizando os parâmetros numéricos:
Então, na situação de tubo fechado a cola deverá resistir a uma força de:
Passo 3
- Considerando tubo aberto
A partir das hipóteses, a equação de balanço apresentada no Passo 1 pode ser escrita como:
Em função das hipóteses do problema, pode-se afirma que o fluxo de quantidade de movimento nas superfícies e são iguais:
Logo:
Sabendo representa as forças de superfície (força devido à pressão e à tensão de cisalhamento), então ela pode ser escrita como:
Nota: sinal positivo no sentido do eixo x.
Então, isolando o termo :
Mas a partir do Passo 2 é conhecido que:
Nota:
Logo, pode-se afirmar que na situação de tubo aberto que:
Resposta
- tubo fechado
- tubo faberto