Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Çengel - Transferência de Calor- Ed: 4º - Capítulo 4.Problemas - Ex. 147
Em uma fábrica, grandes placas de aço inoxidável de 40 cm de espessura são retiradas de um forno a uma temperatura uniforme de 750°C. As placas são colocadas em banho-maria que é mantido a uma temperatura constante de 20°C com um coeficiente de transferência de calor de . O tempo necessário para que a temperatura da superfície caia para 120°C é:
a) 0,6h;
b) 0,8h;
c) 1,4h;
d) 2,6h;
e) 3,2h.
Passo 1
Vamoo que vamooo!!
Primeiro, nós queremos achar o que?
O tempo para que a temperatura da superfície caia para 100°C, certo?
Mas antes de qualquer coisa precisamos saber o número de Biot, para a haste A:
Sabemos que:
Agora nós precisamos do comprimento característico da placa:
Lembrando que:
Então:
Agora é só calcular o Biot:
Como o nós não podemos fazer a análise do sistema agrupado.
E agora?
Simples!! Nós podemos usar outra equação:
Então nós vamos precisar achar e
Passo 2
Olhando a Tabela:
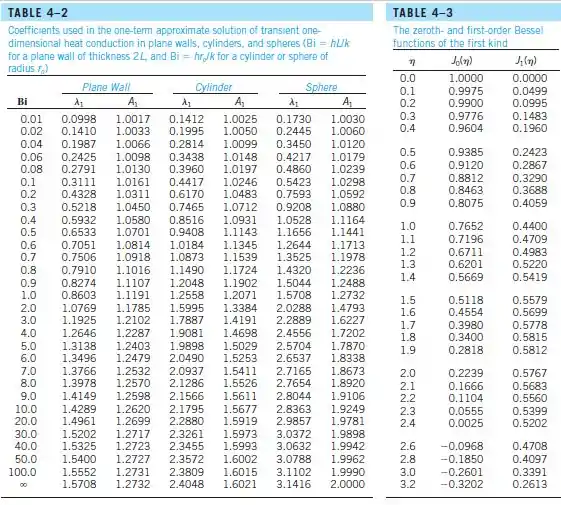
Pela tabela nós achamos que:
Agora que temos a fórmula nós só precisamos ver quais dados nós temos, não é?
Agora é só achar o tempo adimensional, e ele sim está relacionado ao tempo!
Bora então??
Aplicando o ln:
Passo 3
Agora que temos o tempo adimensional, vamos ver como ele se relaciona com o tempo que nós queremos, ok?
Se:
Então:
Em horas:
Então, nossa resposta aqui será a letra (e) !!