Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 5.Problemas - Ex. 58
A resistência e a estabilidade de pneus podem ser melhoradas pelo aquecimento de ambos os lados da borracha (k = 0,14 W/(m · K), α = 6,35× 10−8 m2/s) em uma câmara de vapor na qual T∞ = 200°C. No processo de aquecimento, uma parede de borracha com 20 mm de espessura (suposta não frisada) é levada de sua temperatura inicial de 25°C até uma temperatura no plano central de 150°C.
(a) Se o escoamento do vapor sobre as superfícies do pneu mantém um coeficiente convectivo de h = 200 W/(m2 · K), quanto tempo será necessário para se atingir a temperatura desejada no plano central?
(b) Para acelerar o processo de aquecimento, recomenda-se que o escoamento do vapor seja feito com vigor suficiente a fim de manter as superfícies do pneu a uma temperatura de 200°C durante todo o processo. Calcule e represente graficamente as temperaturas no plano central e nas superfícies do pneu para esse caso, assim como para as condições da parte (a).
Passo 1
Vamos analisar o enunciado juntos e entender o que o problema quer de você.
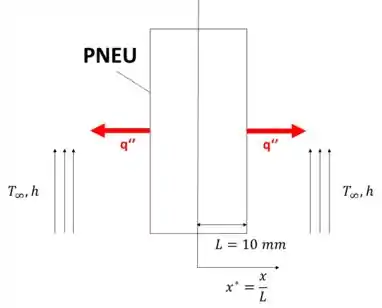
Temos um pneu sendo aquecido em uma câmara de vapor de uma temperatura de 25 a 150 no centro da do pneu. Podemos, então, modelar esse pneu como uma placa plana sofrendo uma transferência de calor transiente com convecção, como demonstra a imagem abaixo:
Por isso, se a gente supor tempos muito longos () podemos modelar a temperatura adimensional no plano central () a partir da equação:
Sendo e coeficientes que podem ser calculados a partir da Tabela 5.1, o adimensional Número de Fourier, a temperatura no centro depois do tempo decorrido, a temperatura inicial e a temperatura do ar.
Pra resolver a primeira parte do problema, devemos calcular o tempo necessário para a temperatura no centro atingir .
Por fim, devemos traçar um gráfico comparativo da evolução da temperatura do centro e da superfície para as condições anteriores e para uma condição em que a temperatura da superfície é de 200 . Devemos usar a seguinte equação para modelar a temperatura adimensional na superfície ():
Sendo e coeficientes que podem ser calculados a partir da Tabela 5.1, o adimensional Número de Fourier, a temperatura na superfície do pneu, a temperatura inicial e a temperatura do ar.
Agora, pra gente não se perder, vamos guardar as propriedades que vamos usar nos próximos passos:
Passo 2
Vamos resolver o item (a).
Primeiro, devemos calcular o número de Biot para o problema:
Vamos agora na Tabela 5.1 para calcular os valores dos coeficientes de e para a parede plana. Como podemos ver na tabela, não temos o valor de tabelado. Devemos, então, fazer uma interpolação entre os valores de e :
Portanto, interpolando:
Vamos deixar o número de Fourier em função do tempo :
Vamos substituir os valores que encontramos no Passo 2 na primeira equação que deduzimos no Passo 1:
Além disso, devemos lembrar que:
Igualando os dois resultados:
Vamos aplicar em ambos os lados da equação:
Vamo agora calcular o número de Fourier pra confirmar que nossa suposição de tempos longos tá certa:
Logo, nossa suposição estava certa.
Passo 3
Vamos finalizar a questão resolvendo o item (b).
Para as condições do item (a), vamos escrever dois modelos em função do tempo, um da temperatura da superfície ( e um da temperatura do centro ():
Além disso, devemos calcular o valor de para uma condição de temperatura na superfície , a partir da equação abaixo:
Sabemos que e , portanto, obtemos:
Se aplicarmos a ambos os lados da equação:
Se formos na Tabela 5.1 para a parede plana, temos que para , encontramos:
Como , , influenciando na temperatura da superfície do pneu.
Agora sim, podemos deixar a temperatura do centro nessas condições () em função do tempo:
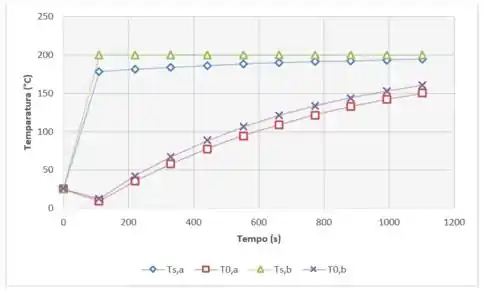
Agora podemos ir no Excel e plotar essas equações em função do tempo indo de 0 a , que é o tempo de processo que calculamos no passo anterior:
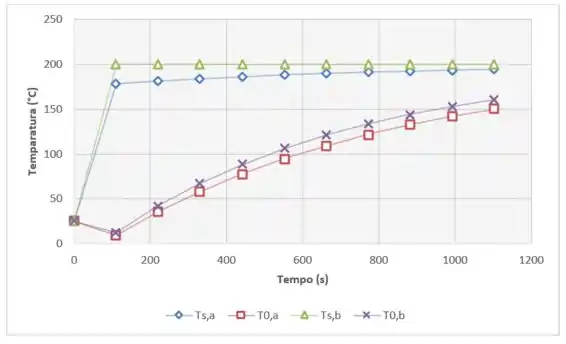
Resposta
(a) O tempo necessário para a temperatura no plano central atingir .
(b)
