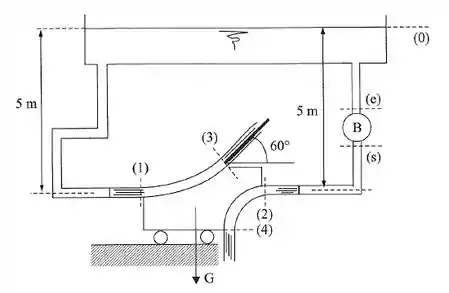
Dados ; . Calcular:

a) a potência no eixo da bomba para que o corpo apoiado nas rodas sem atrito permaneça parado;

b) a força que o corpo exerce sobre o solo, sendo o seu peso .

(Desprezar o peso do trecho (1)-(3) do jato.)

Agora vamos aplicar a equação para a força exercida pelo fluido novamente, só que entre os trechos 2 e 4, dessa forma, a equação se torna:

Vamos aplicar a equação na direção :

Podemos escrever a vazão mássica como:

Substituindo essa expressão na equação para a força, temos:

Para que o carrinho permaneça parado, então a força da esquerda e da direita devem ser iguais, dessa forma, temos:

Substituindo os valores conhecidos, temos:

Agora vamos aplicar o equilíbrio de cargas entre os pontos 0 e 2:

Substituindo os valores conhecidos:

Agora vamos calcular a vazão na parte do sistema que contém a bomba através de:

E, com a vazão, podemos finalmente encontrar a potência da bomba, dada por:

Agora para resolver a letra b), vamos usar novamente a equação da força exercida pelo fluido entre os pontos 1 e 3:

Só que agora vamos aplicar a equação na direção :

Como a vazão é constante e o diâmetro do jato também, então temos , e podemos escrever a vazão mássica como:

Substituindo essa expressão na equação para a força, temos:

Substituindo os valores conhecidos, temos:

Agora vamos aplicar a equação para a força exercida pelo fluido novamente, só que entre os trechos 2 e 4, dessa forma, a equação se torna:

Vamos aplicar a equação na direção :

Como a vazão mássica é constante e o diâmetro do jato também, então temos . E podemos escrever a vazão mássica como:

Substituindo essa expressão na equação para a força, temos:

Substituindo os valores conhecidos, temos:

Assim, a força resultante no solo será: