Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 13.Problemas - Ex. 94

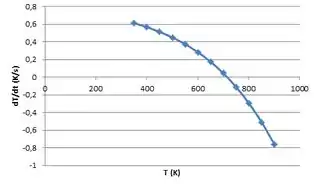
Uma placa cinza, difusa e opaca ( 200   m m   x   200   m m ) , com uma emissividade de 0,8, é colocada sobre a abertura de um forno e sabe-se que, em um determinado instante, ela se encontra a 400 K. A base do forno, que tem as mesmas dimensões da placa, é negra e opera a 1000 K. As paredes laterais do forno são isoladas termicamente. A parte superior da placa está exposta ao ar ambiente, com um coeficiente de transferência de calor por convecção de 25 W m 2 K , e a uma grande vizinhança. O ar e a vizinhança estão a 300 K.

  1. Calcule a transferência radiante líquida para a superfície inferior da placa.
  2. Se a placa tem uma massa e um calor específico de 2 kg e 900 J k g K , respectivamente, qual será a variação da temperatura da placa com o tempo, d T p d t ? Suponha que a transferência de calor por convecção na superfície inferior da placa seja desprezível.
  3. Estendendo a análise da parte (b), gere um gráfico da variação da temperatura da placa com o tempo, d T p d t , como uma função da temperatura da placa para 350   ≤ T p ≤   900   K . Todas as demais condições permanecem as mesmas. Qual é a temperatura da placa em condições de regime estacionário?

Passo 1

Shoow de bola galerinhaaa !!

Vamos continuar?

Começando pela letra (a) nós temos que calcular a transferência radiante líquida para a superfície inferior da placa, certo?

Para isso nós precisamos lembrar que a placa ( A 1 ), o fundo do forno ( A 2 ) e as paredes laterais do forno ( A R ) formam um gabinete de três superfícies com uma superfície sendo rerradiante, neste caso nós podemos usar a fórmula:

q 1 = E b , 1 - E b , 2 1 - ε 1 ε 1 A 1 + 1 A 1 F 12 + 1 A 1 F 1 R + 1 A 2 F 1 R - 1 + 1 - ε 2 ε 2 A 2

Vamos ver o que sabemos?

ε 1 = 0,8

ε 2 = 1

A área nós também sabemos, não é?

A 1 = A 2 = 0 , 2   m   x   0 , 2   m = 0,04   m 2

As potências emissivas nós sabemos calcular, não é?

E b 1 = σ T 1 4

E b 2 = σ T 2 4

Lembrando que:

σ = 5,67 × 10 - 8   W m 2 K 4

T 1 = 4 0 0   K

T 2 = 10 00   K

Então:

E b 1 = 5,67 × 10 - 8   W m 2 K 4 40 0   K 4 = 145 4   W m 2

E b 2 = 5,67 × 10 - 8   W m 2 K 4 10 00   K 4 = 56700   W m 2

Agora só nos resta achar os fatores de forma, não é?

Passo 2

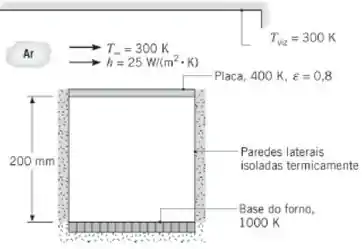
Para achar o fator de forma entre 1 e 2 vamos dar uma olhada na figura abaixo:

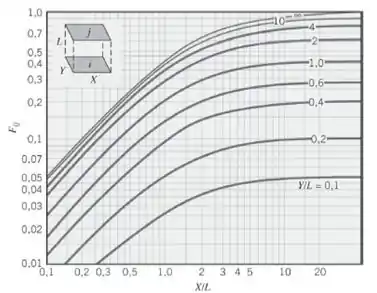
Lembrando que:

X = Y = L = 200   m

Então:

X L = Y L = 200   m m 200   m m = 1

No gráfico:

F 12 = 0,2

Agora podemos aplicar a soma para a superfície 1:

F 12 + F 1 R = 1

F 1 R = 0,8

Por simetria:

F 2 R = 0,8

Agora podemos só colocar tudo na fórmula do Passo 1:

q 1 = 1454   W m 2 - 56700   W m 2 1 - 0,8 0,8 × 0,04   m 2 + 1 ( 0,04   m 2 × 0 , 2 ) + 1 0,04   m 2 × 0,8 + 1 0,04   m 2 × 0,8 - 1 + 1 - 1 1 × 0,04   m 2

q 1 = - 1153,027   W

Finalizamos a letra (a) !!

Passo 3

Na letra (b) nós queremos achar a variação da temperatura da placa com o tempo, d T 1 d t , sabendo que:

  m = 2   k g

c p = 900 J k g K

Neste caso nós vamos começar aplicando o balanço energético:

q r a d ,   f - q c o n v - q r a d ,   v i z = m c p d T 1 d t

Aqui, q r a d ,   f é a transferência de calor por radiação entre a placa e o forno, q c o n v a transferência de calor por convecção na parte superior do forno e q r a d ,   v i z a taxa de transferência de calor por radiação entre a placa e o ambiente!

Sabemos que:

q r a d ,   f = q 1 = 1153,027   W

q c o n v = h A 1 T 1 - T ∞

q r a d ,   v i z = ε 1 σ T 1 4 - T ∞ 4

Na fórmula:

1153,027   W - h A 1 T 1 - T ∞ - ε 1 σ T 1 4 - T ∞ 4 = m c p d T 1 d t

Se temos todos os dados, como mostrado na figura, vamos só substituir:

1153,027   W - 25 W m 2 K 0,04   m 2 400   K - 300   K - 0,8 5,67 × 10 - 8   W m 2 K 4 400   K 4 - 3 00   K 4 = 2   k g 900 J k g K d T 1 d t

Resolvendo:

d T 1 d t = 0,567 K s

Legal, não foi ?!

Bora pra (c) ??

Passo 4

Na letra (c) nós queremos gerar um gráfico da variação da temperatura da placa com o tempo, d T 1 d t , como uma função da temperatura da placa para 350   ≤ T 1 ≤   900   K .

Faremos o Passo 3 todo novamente para cada T 1 , tudo bem?

Podem usar um software que vai facilitar:

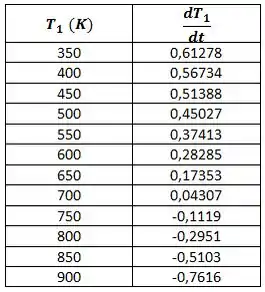
Plotando o gráfico:

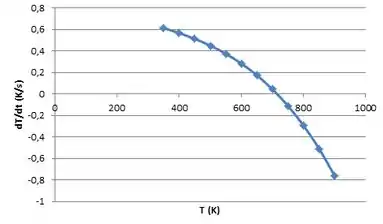
Para que a placa esteja no estado estacionário teremos que ter:

d T d t = 0

Colocando este valor na equação do Passo 3 e resolvendo:

T e s t .   e s t . = 715   K

E é isso aí galerinha, bora seguir ??

Resposta

  1. - 1153,027   W ;
  2. d T 1 d t = 0,567 K s ;
  3. T e s t .   e s t . = 715   K ;

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Dois objetos convexos estão no interior de um grande recipiente, no qual há vácuo. As paredes do recipiente são mantidas a T 3=300K . Os objetos têm a mesma área, igual a 0,2m 2 , e a mesma emissivida
Considere a cavidade composta por quatro superfícies cinzas e difusas, com todos os lados iguais, mostrada na figura. As temperaturas de três superfícies são especificadas, enquanto a quarta encontra-
Uma sala é representada pela cavidade a seguir, onde o teto (1) tem uma emissividade de 0,8 e é mantido a 40°C por elementos aquecedores elétricos nele embutidos. Também são usados aquecedores para ma
Um forno cilíndrico usado para o tratamento térmico de materiais no ambiente de uma nave espacial tem um diâmetro de 90 mm e um comprimento total de 180 mm. Os elementos aquecedores, na seção com 135
Um forno de laboratório tem uma câmara interna cúbica com 1 m de lado, com superfícies interiores com emissividade ε = 0,85. Determine a taxa de transferência de calor radiante inicial para o laborató