Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 12.Problemas - Ex. 143

Uma fina camada de água está exposta ao ambiente natural, conforme mostrado na figura.

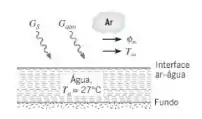
Considere condições nas quais as irradiações solar e atmosférica são GS = 600 W/m2 e Gatm = 300 W/m2 , respectivamente, e a temperatura e a umidade relativa do ar são T∞ = 27°C e ϕ∞ = 0,50, respectivamente. As refletividades da superfície da água em relação às irradiações solar e atmosférica são ρS = 0,3 e ρatm = 0, respectivamente, enquanto a emissividade superficial é ε = 0,97. O coeficiente de transferência de calor por convecção na interface ar–água é h = 25 W/(m2 · K). Se a água está a 27°C, essa temperatura irá aumentar ou diminuir com o passar do tempo?

Passo 1

Fala aí! Partiu resolver essa questão aí! Precisamos dizer se a temperatura vai aumentar ou diminuir… Show! Mas antes de ir para as contas, precisaremos de alguns dados adicionais, que podemos pegar no apêndice do livro, tabela A-4, com T = 300   K :

ρ A = 1,161   k g / m ³ c p ,   a = 1007   J / k g . K P r = 0,707

Na tabela A-6, para a água, com T = 300   K :

ρ w = 997   k g / m ³ c p ,   w = 4179   J / k g . K

Para vapor, com T = 300   K :

ρ A ,   s a t = 0,0256   k g / m ³ h f g = 2,438   .   10 6   J / k g

E na tabela A-8, com T = 300   K :

D A B ≈ 0,26   .   10 - 4   m ² / s v a = 15,89   .   10 - 6   m ² / s

S c = v a D A B = 15,89   .   10 - 6 0,26   .   10 - 4 = 0,61

Passo 2

Agora partiu continhas, ok?

Vamos descobrir o que ele quer fazer uma relação, usando o nosso balanço de energia, teremos o seguinte:

E s t = G S ,   a b s + G A ,   a b s - E - q e v a p "   .   A

d ρ w   .   c p ,   w   .   L   .   A   .   T w d t = 1 - ρ S   .   G S + 1 - ρ A   .   G A - ε   .   σ   .   T w 4 - h m   .   h f g   .   ρ A ,   s a t - ρ A ,   ∞   .   A

Considerando T ∞ = T w e sendo ρ A ,   ∞ = φ ∞   .   ρ A ,   s a t , teremos:

ρ w   .   c p ,   w   .   L   .   d   T w d t   =   1 - ρ S   .   G S + 1 - ρ A   .   G A - ε   .   σ   .   T w 4 - h m   .   h f g   .   1 - φ   ∞ .   ρ A ,   s a t

Pra gente descobrir quem é o h m , podemos usar a equação 6.60, sendo n = 1 3 , ficaremos com:

h m = h ρ a   .   c p ,   a   .   L e 1 - n

h m = h ρ a   .   c p ,   a   .   S c P r 1 - n

h m = 25 1,161   .   1007   .   0,61 0,707 1 - 1 3

h m = 0,0236   m / s

Agora simmm! Vamos voltar lá na equação e achar o que precisamos!

ρ w . c p ,   w . L . d   T w d t = 1 - 0,3 . 600 + 1 - 0 . 300 - 0,97.5,67 . 10 - 8 . 300 4 - 0,0236.2,438 . 10 6 . 1 - 0,5 . 0,0256

ρ w . c p ,   w . L . d   T w d t =   - 461   W / m ²

Uhull! Conseguimos! Como nosso resultado deu negativo, vemos que a água vai esfriar, ou seja, a temperatura irá diminuir… Arrasamos!

Resposta

A temperatura vai diminuir.

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Considere um duto longo semicilíndrico de 1 m de diâmetro. O calor é fornecido a partir da superfície da base, que é negra, a uma taxa de 1200 W/m², enquanto a superfície lateral com emissividade de 0
Dois discos pretos paralelos estão posicionados coaxialmente com distância de 0,25 m entre eles em um ambiente de temperatura constante de 300 K. O disco inferior tem 0,2 m de diâmetro e o disco super
Em uma caldeira que queima gás natural, gases de combustão passam por tubos de 6m de comprimento e 15c m de diâmetro, imersos em água a 3a t m de pressão. A temperatura dos tubos é medida como sendo 1
Em uma caldeira que queima gás natural, gases de combustão passam por tubos de 6m de comprimento e 15c m de diâmetro, imersos em água a 1a t m de pressão. A temperatura dos tubos é medida como sendo 1
Dois cilindro concêntricos muito longos de diâmetros D 1 = 0,35m e D 2 = 0,5m são mantidos a temperatura uniformes de T 1 = 950K e T 2 = 500k e têm emissividade ε 1 = 1 , ε 2 = 0,55 , respectivamente.