Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 7.Problemas - Ex. 24
Placas de aço (AISI 1010), de espessura e lados com comprimento , são transportadas na saída de um processo de tratamento térmico e simultaneamente resfriadas por ar atmosférico com velocidade e em escoamento paralelo sobre as placas.
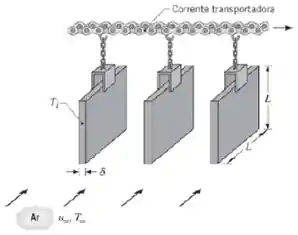
Para uma temperatura da placa inicial de , qual é a taxa de transferência de calor saindo da placa? Qual é a taxa de variação da temperatura da placa correspondente? A velocidade do ar é muito maior que a velocidade da placa.
Passo 1
É sempre importante começarmos estas questões com as nossas hipóteses para o problema. Neste caso, temos propriedades constantes do ar, placas isotérmicas e não iremos considerar a convecção na parte lateral da placa.
Nosso primeiro passo é determinar a taxa de transferência de calor saindo da placa. Como temos um problema que envolve regime transiente, vamos calcular a taxa inicial, considerando .
Portanto, esta taxa será dada por:
Destaque para o número 2 na frente!!! Não podemos esquecer dele pois estamos considerando convecção nos dois lados da placa (frente e atrás).
Então, o nosso trabalho será determinar o coeficiente médio de transferência de calor.
Mas, antes disto, vamos aproveitar para obter as propriedades do ar e da placa. Consideraremos que o ar está a 1 atm e a temperatura do filme é , enquanto a placa está a .
Utilizando a tabela , temos: , , . Detalhe que obtivemos todos os dados a partir da interpolação da tabela.
Já em relação a placa, da tabela , temos: , , .
Passo 2
Agora, vamos calcular o coeficiente de transferência de calor. Para isto, precisamos saber qual a correlação correta para o número de Nusselt. E para isto, precisamos do número de Reynolds.
Então, temos:
Como temos , estamos trabalhando com escoamento laminar. Portanto, A correlação correta para o número de Nusselt será:
Portanto, a taxa de transferência de calor é:
Passo 3
Agora iremos calcular a taxa de variação de temperatura no tempo. Para isto, vamos fazer um balanço de energia em torno da placa. Portanto,
Como não entra energia na placa e nem é gerado nada, temos apenas o termo de energia que sai e o termo de energia acumulada.
Detalhe é que o termo de energia que sai é exatamente o que calculamos no final do passo anterior! Um alívio a mais para a gente!
Agora, basta substituir o termo de energia acumulada e isolar o termo de variação de temperatura no tempo para finalizar a questão. Sendo assim, temos:
E assim finalizamos a questão!