Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 6.Problemas - Ex. 107
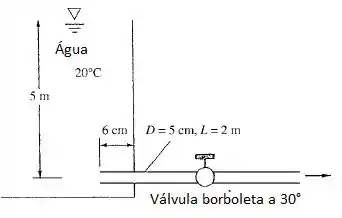
Na figura abaixo o tubo é de aço galvanizado. Calcule o percentual de aumento na vazão (a) se a entrada do tubo for cortada rente à parede do reservatório e (b) se a válvula borboleta estiver totalmente aberta.
Passo 1
E aí, gente!! Tudo bem? Então vou mostrar pra vocês que mecânica dos fluidos não é nem de longe um bicho de 7 cabeças (nem de perto também)!
Primeiro vamos logo pegar as propriedades da água em 20°C, show?
Além disso, vamos também procurar a rugosidade desse trem aí que é o aço galvanizado. Vou te adiantar essa parte pra você não precisar ficar que nem doido procurando no livro hehe
Opa, então com isso já podemos calcular qual deve ser a rugosidade relativa, que é:
Bem, quanto equivale o L/D e o K de uma entrada do tubo igual essa no tanque? Vai na figura 6.21a do livro que você vai ver que
Para a válvula borboleta com 30°, a figura 6.19 do livro vai te mostrar que
Passo 2
Bora escrever nossa equação de Bernoulli?
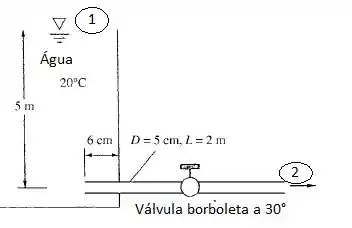
Bem, para os nossos dois pontos escolhidos no nosso sistema, temos que , então esses termos se cancelam, certo? Vamos então escrever de forma a isolar a diferença de altura, beleza?
Outra hipótese que costumamos usar é que a velocidade de um fluido em sua superfície exposta à atmosfera é aproximadamente zero, ou seja,
Onde se refere as perdas de cargas maiores e o termo relacionado à perdas menores!!
Passo 3
De posso da nossa equação de Bernoulli simplificada, podemos então agora abrir esses termos todos referentes às perdas de carga!!
Note que vamos precisar “chutar” f, uma vez que ele depende de Reynold, que por sua vez depende da velocidade, a qual é nossa variável!!! Que tour né kkk, mas vamos lá!
Vamos chutar , porque? Ah, porque eu quis, poderia ser qualquer outro valor!! Note que com esse valor de f, teremos ao final que:
E por consequência
Passo 4
Quais seriam os próximos passos? Bem, agora seria um cálculo iterativo, onde com esse valor de Re, juntamente com o valor de rugosidade relatividade que encontramos lá no passo 1, iríamos no diagrama de Moody.
No diagrama, você pegaria um novo valor de f, jogaria na equação simplificada de Bernoulli do passo 2 e 3, encontraria um novo valor de velocidade e por fim, um novo valor de Reynold.
Você teria que fazer esse processo até convergir.
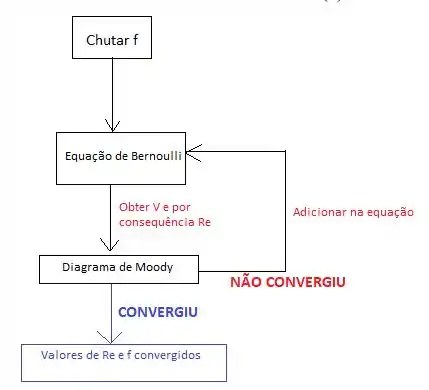
Fazendo esse processo, você verá que e
Ou seja, com essa velocidade convergida, calculamos a vazão sendo
Passo 5
(a) Se a gente fizesse um corte rente a entrada do tanque, o que acontece é que o K da entrada se reduziria a metade, ou seja,
O que bastaria com que pegássemos a equação que já usamos no passo 3 e precisaríamos mudar o valor de para 0,5.
Note que isso é uma redução muito pequena! Porque eu tô te falando isso? Porque na prática você teria que refazer o mesmo processo de convergência que fez anteriormente. Mas como é uma redução muito pequena de K, podemos aproximar f ao valor que encontramos no passo anterior. Dessa forma, vamos obter uma velocidade de
O que causará uma vazão de , ou seja, 0,3% a mais!
Passo 6
(b) Se a válvula borboleta abrir por completa, o seu . Note que esse valor já foi uma queda muito abrupta do valor que estávamos usando anteriormente, ou seja, aqui não poderemos simplesmente explicitar f como sendo o que encontramos anteriormente. Precisaríamos montar a equação de Bernoulli
Chutar um valor de f, vou continuar chutando f=0,02 e fazer o mesmo processo de convergência para encontrar a velocidade.
Ao final desse processo, você observará que , fazendo nossa vazão subir pra caramba!!!
Resposta
- 0,3 %
- 5 vezes mais!