Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 3.Problemas - Ex. 133
O tubo longo da Figura P3.133 está cheio de água a 20C. Quando a válvula A está fechada, . Quando a válvula é aberta e a água escoa a 500 m³/h, . Qual é a perda de carga por atrito entre 1 e 2, em m, para a condição de escoamento?
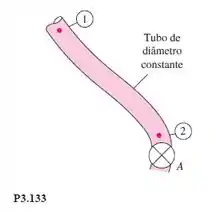
Passo 1
Bora pra mais uma!!
Vamos primeiro considerar o momento em que a válvula está fechada, nesse momento não haverá perda de carga por atrito e nem velocidade. Daí, da equação da energia:
Agora, vamos considerar o momento onde a válvula está aberta e o fluido escoa em regime permanente, nesse momento, a velocidade no ponto 1 é igual a velocidade no ponto 2. Daí, da equação de energia temos:
Resposta
A perda de carga por atrito entre 1 e 2 é de 8,7m.
Exercícios de Livros Relacionados
Trace o gráfico da velocidade do ar versus a pressão dinâmica (em milímetros de mercúrio) para uma pressão dinâmica de até 250 mmHg.
Água escoa com velocidade de 3 m/s. Calcule a pressão dinâmica deste escoamento. Expresse sua resposta em polegadas de mercúrio.
A água escoa em regime permanente para cima no interior do tubo vertical de 0,1 m de diâmetro e é descarregada para a atmosfera através do bocal que tem 0,05 m de diâmetro. A velocidade média do escoa
Você (um jovem com idade permitida para beber) está fazendo cerveja caseira. Como parte do processo, você deve sugar o mosto (a cerveja fermentada com sedimentos no fundo) de um tanque limpo por meio
O seu carro fica sem combustível inesperadamente. Para você resolver o problema, você retira gasolina de outro usando um sifão. A diferença de altura do sifão é cerca de 150 mm. O diâmetro da mangueir