Foi sugerido, no projeto de um “sprinkler” agrícola, que um elemento estrutural fosse mantido fixo por meio de um arame esticado ao longo da linha de centro de um tubo; acreditava-se que um arame relativamente fino teria pouco efeito sobre a queda de pressão para uma dada vazão. Usando o resultado do Problema 8.56, deduza uma expressão que dê a variação percentual em queda de pressão como uma função da razão entre o diâmetro do arame e o diâmetro do tubo para escoamento laminar. Trace um gráfico da variação percentual na queda de pressão como uma função da razão de raios para 0,001 0,10.
Passo 1
O problema a ser avaliado exigirá o uso da expressão de vazão obtida na questão 8.56 (escoamento laminar completamente desenvolvido em espaço anular formado por dois cilíndricos, especificamente o tubo e o arame):
A partir da expressão de é pedida a variação percentual de queda de pressão. Sabendo das características do escoamento (escoamento completamente desenvolvido em tubo), a queda de pressão ao longo do tubo é dada por:
Já a variação de pressão pode ser escrita como:
Passo 2
O cálculo da queda de pressão exigirá escrever o termo a partir da expressão da vazão:
Então, a queda de pressão ao longo do tubo, para é:
Já para (valor de tendendo a zero) a queda de pressão é expressa por:
O termo , quando , é um valor que cresce tendendo ao infinito, de forma que:
Assim:
Passo 3
Calculando a variação percentual da queda de pressão:
E sabendo as expressões de e , tem-se que:
Realizando o mínimo múltiplo comum:
Passo 4
Em considerando muito pequeno (conforme apresentado pelo enunciado) a expressão da variação de queda de pressão obtida no Passo 3 pode ser simplificada, pois:
Assim:
É possível reescrever o termo :
Então, conclui-se que para muito pequeno a variação de queda de pressão é dada por:
Considerando, em termos percentuais, a variação de queda de pressão é definida como:
Passo 5
Considerando o intervalo de para 0,001 0,10 (valor muito pequeno) é possível avaliar o comportamento da variação de queda de pressão com a alteração de , segundo expressão obtida no Passo 4, conforme a Tabela e Figura que se seguem:
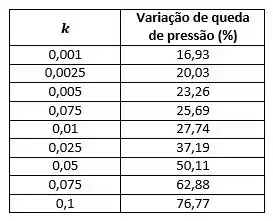
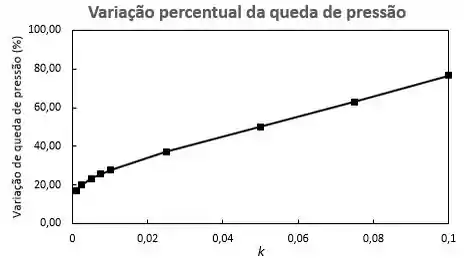
Resposta
Para muito pequeno a expressão da variação percentual de queda de pressão é dada por: