Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 8º - Capítulo 1.Problemas - Ex. 43

For the fl ow of gas between two parallel plates of Fig. 1.7,

reanalyze for the case of slip fl ow at both walls. Use the

simple slip condition, δuwall 5

the mean free path of the fl uid. Sketch the expected velocity profi le and fi nd an expression for the shear stress at

each wall.

Passo 1

Saaaalve, tranquilo? Vamos lá resolver mais uma questão juntos?! 😊

Calculando a condição de deslizamento nas paredes paralelas das placas:

δ u p a r e d e = l d u d y p a r e d e

Aqui, U é a velocidade da placa se movendo

Calculando a distribuição linear da velocidade

u y = a + b y

Passo 2

Devido à condição de deslizamento a velocidade do gás na placa inferior é δ u p a r e d e

Já que a placa superior está se movendo com uma velocidade de U . A velocidade do gás adjacente para a placa superior é menor que a velocidade da placa superior por δ u p a r e d e , devido a condição de deslizamento.

Calculando a velocidade do gás adjacente à placa superior

u y y = h = U - δ u y = h

Passo 3

Desenhando o fluxo do gás entre as duas placas paralelas

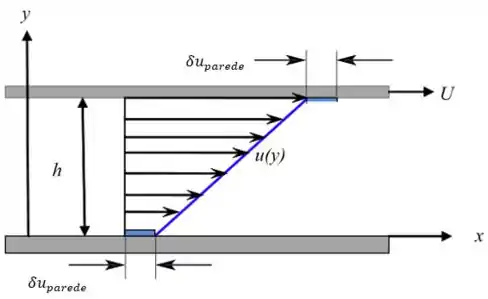
Passo 4

Aplicando as condições de fronteira nas paredes

Parede inferior:

Em y = 0

u y y = 0 = δ u

→ a + b y y = 0 = l d u d y

→ a + b ⋅ 0 = l d a + b y d y

∴ a = l b

Parede superior:

Em y = h

u y y = h = U = δ u y = h

→ a + b y y = h = U - l d u d y y = h

→ a + b ⋅ h = U - l d a + b y d y y = h

→ a + b h = U - l b

∴ b = U 2 l + h

Passo 5

Temos que

a = l b

Substituindo o que achamos

a = l U 2 l + h = U l 2 L + h

Substituindo na equação para u y

u y = a + b y = U l 2 L + h + U 2 L + h y

→ u y = U l 2 l + h l + y

Passo 6

Calculando a tensão de cisalhamento

τ = μ d u d y

Substituindo valores

τ = μ d d y U l 2 l + h l + y

→ τ = U μ 2 l + h

Passo 7

Tensão de cisalhamento na parede inferior

Para a tensão de cisalhamento na parede substituímos h = 0

τ = U μ 2 l + 0

∴ τ = U μ 2 l

Tensão de cisalhamento na parede superior

Para a tensão de cisalhamento na parede substituímos h = h

∴ τ = U μ 2 l + h

Resposta

τ = U μ 2 l

τ = U μ 2 l + h

Exercícios de Livros Relacionados

A viscosidade pode ser medida pelo escoamento através de um tubo de diâmetro pequeno ou de um tubo capilar, se a vazão for baixa. Para um comprimento L, (pequeno) diâmetro D Δ p e (baixa) vazão em vol
Um instrumento popular acionado por gravidade é o viscosímetro Cannon-Ubbelohde, mostrado na Figura A1.10. O líquido de teste é succionado para cima do bulbo no lado direito e deixado drenar por gravi
Para o campo de tensão bidimensional da Figura P2.1 sabe-se que σ x x = 143640 N m 2σ y y = 95760 N m 2e σ x y = 23940 N m 2 Encontre as tensões de cisalhamento e normal (em N / m 2 ) que atuam sobre
Para o campo de tensão bidimensional da Figura P2.1 sabe-se que σ x x = 9576 0 N m 2σ y y = 143640 N m 2e σ n ( A A ) = 119700 N m 2 Calcule (a) a tensão de cisalhamento σ X Y e (b) a tensão de cisalh
Na Figura 1.8 , se o fluido é glicerina a 20° C e a distância entre as placas é 6m m , qual é a tensão de cisalhamento (em P a ) necessária para mover a placa superior a 5,5m / s ? Qual é o número de