Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 1.Problemas Abrangentes - Ex. 10

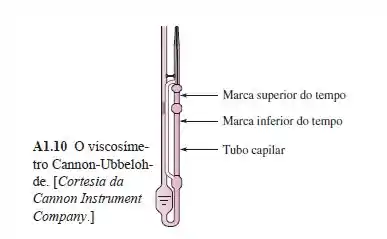
Um instrumento popular acionado por gravidade é o viscosímetro Cannon-Ubbelohde, mostrado na Figura A1.10. O líquido de teste é succionado para cima do bulbo no lado direito e deixado drenar por gravidade através do tubo capilar abaixo do bulbo. É registrado o tempo t necessário para o menisco passar da marca superior para a inferior. A viscosidade cinemática é calculada pela fórmula simples:

ν = C t

na qual C é uma constante de calibração. Para ν no intervalo de 100 m m 2 / s a 500 m m 2 / s , a constante recomendada é C = 0,50   m m 2 / s , com uma precisão menor que 0,5 % .

  1. Quais os líquidos da Tabela A.3 que estão neste intervalo de viscosidade? (b) A fórmula de calibração é dimensionalmente consistente? (c) De quais propriedades do sistema pode depender a constante C? (d) Qual o problema deste capítulo que traz uma fórmula para cálculo da viscosidade?

Passo 1

Bora pra essa!

Olhando a tabela A.3, analisando pela viscosidade cinemática chegaremos que apenas 3 dos líquidos estão dentro do intervalo, sendo eles os óleos SAE 10W, 10W30 e 30W, com, respectivamente, 120   m m 2 / s , 194   m m 2 / s e 326   m m 2 / s .

Passo 2

Ao analisarmos a fórmula, podemos ver que ela não é dimensionalmente consistente pois, a unidade de viscosidade cinemática é m m 2 / s e C tem a mesma dimensão da viscosidade, coisa que não deveria acontecer pois está multiplicando por t.

Passo 3

A constante C pode depender do tamanho e diâmetro do tubo, além da aceleração da gravidade, visto que a viscosidade cinemática também pode sofrer com esses fatores!

Passo 4

O problema P1.58 nos traz uma fórmula para cálculo da vazão no tubo. Se a vazão estiver sendo vertical e impulsionado pela gravidade, teremos que:

ν ≈ g d 2 32 V

Isso por conta das seguintes expressões:

Δ p = ρ g L           e         Q = π 4 d 2 V

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Para o campo de velocidade em que V → = A x 2 y i ^ + B x y 2 j ^ , em que A = 2m - 2 s - 1 e B = 1m - 2 s - 1 , e as coordenadas são medidas em metros, obtenha uma equação para as linhas de corrente
Ocampodevelocidadeemque V → A x i ^ - A y j ^ , em que A = 2 s - 1 , pode ser interpretado para representar o escoamento em um canto.Determineumaequaçãoparaaslinhasde corrente do escoamento. Trace div
Umescoamentoédescritopelocampodevelocidade V → = A x + B i + - A y j , em que A = 3 m m m e b = 6 m s . Trace algumas linhas de corrente no plano x y , incluindo aquela que passa pelo ponto x , y = 0,
Paraoscamposdevelocidadedadosabaixo,determine: a.Seocampodeescoamentoéuni,bioutridimensional,eporquê. b.Seoescoamentoéemregimepermanenteoutransiente,eporquê.(Asquantidadesaebsãoconstantes.) 1 → V = a
Umlíquidoviscosoécisalhadoentredoisdiscosparalelos;odiscosuperiorgiraeoinferioréfixo.Ocampodevelocidadeentreos discosédadopor → V=ê θ ω z / h ê .(Aorigemdascoordenadasestálocalizadanocentrododiscoinfe