Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 8.Problemas - Ex. 70
Mostre que o potencial complexo representa o escoamento em torno de uma oval localizada a meio caminho entre duas paredes paralelas . Qual seria a aplicação prática?
Passo 1
E aí, tudo bem? Bora matar essa questão!
Vamos derivar essa função! Assim temos:
Passo 2
Agora que temos nossa função só precisamos fazer o esqueminha das linhas de corrente, assim temos:
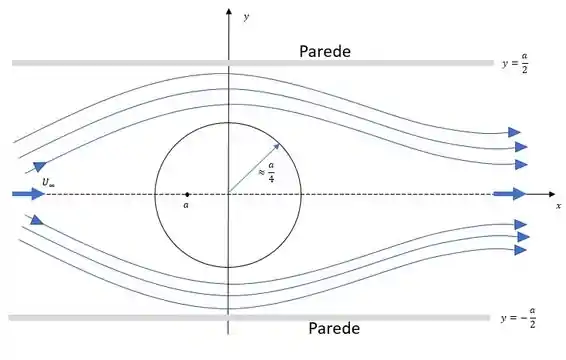
Passo 3
Temos uma aplicação de estudo, avaliando os efeitos de “bloqueio” do escoamento para um escoamento interno com obstáculo!
Isso é tudo pessoal, conseguimos mais uma! \o/
Resposta
Gráfico vide passo a passo.
Temos uma aplicação de estudo, avaliando os efeitos de “bloqueio” do escoamento para um escoamento interno com obstáculo!
Exercícios de Livros Relacionados
Seja o vetor G → ser dado por G → = 4 x z i → - y 2 j → + y z k → e seja V o volume de um cubo de aresta unitária com seu vértice na origem, limitado por x = 0 a 1, y =0 a 1 e z = 0 a 1 (Fig. P9–9). A
Neste capítulo nós deduzimos a equação de continuidade de duas maneiras: usando o teorema da divergência e somando as vazões em massa através de cada face de um volume de controle infinitesimal. Expli
Se um campo de escoamento é compressível, o que podemos dizer sobre a derivada material da densidade? E se o campo de escoamento for incompressível?
Verifique se o campo de velocidade bidimensional, incompressível, permanente do Problema 9-16 satisfaz a equação de continuidade. Fique nas coordenadas cartesianas e mostre todo o seu trabalho.
No Exemplo 9–6, derivamos a equação para taxa de deformação volumétrica 1 V d V d t =∇ →.V → . Escreva isso como uma equação em palavra e discuta o que acontece com o volume de um elemento fluido à me