Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 8.Problemas - Ex. 61
Trace as linhas de corrente da Equação no quadrante superior direito para . Como a velocidade aumenta com ao longo do eixo a partir da origem? Para que ângulo do canto e valor de esse aumento seria linear em ? Para que ângulo do canto e valor de esse aumento seria com ?
Passo 1
E aí, tudo bem? Bora matar essa questão!
Antes de tudo, vamos calcular o ângulo de deflexão:
Para o coeficiente , teremos um escoamento de canto com vamos fazer um esqueminha baseado na figura .
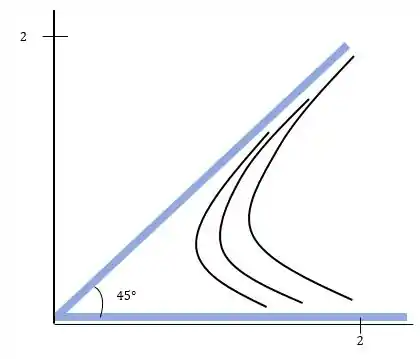
Passo 2
Agora vamos encontrar :
Ao longo do eixo temos que:
De maneira geral:
Passo 3
Seguindo a regra anterior, temos:
Como queremos que o sistema seja linear:
Da figura :
Passo 4
Pra matar nossa questão de vez, temos que:
Como queremos algo elevado a quinta potência, .
Por fim:
Isso é tudo pessoal, conseguimos mais uma! \o/
