A força de propulsão F de uma hélice livre, de um avião ou de um navio, depende da massa específica r, da velocidade de rotação n em r/s, do diâmetro D e da velocidade de avanço V. Os efeitos viscosos são pequenos e desprezíveis aqui. Testes feitos com um modelo de hélice de avião com 25 cm de diâmetro, em um túnel de vento ao nível do mar, resultaram nos seguintes dados de propulsão a uma velocidade de 20 m/s:
![]()
(a) Use esses dados para fazer um gráfico adimensional simples, mas eficaz. (b) Use os dados adimensionais para prever a propulsão, em newtons, de um protótipo de hélice semelhante, com 1,6 m de diâmetro girando a 3.800 r/min e voando a 410 km/h a uma altitude padrão de 4.000 m.
Passo 1
Para a letra “a” vamos utilizar o Teorema Pi de Buckingham para encontrar uma expressão adimensional:
As dimensões dos parâmetros neste caso são:
Logo, nós temos quatro parâmetros (n=5) e três dimensões () (j=3), ou seja, teremos () dois pi grupos:
Resolvendo o sistema linear temos:
Logo:
Para o segundo pi grupo:
Resolvendo o sistema linear temos:
Logo:
Sendo assim:
Agora iremos fazer o gráfico adimensional. Antes vamos montar uma outra tabela com três linhas, a primeira linha terá os valores de n convertidos para r/s, a segunda linha os valores de e a terceira linha os valores de (vamos usar ).
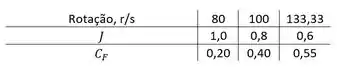
Traçando um gráfico:
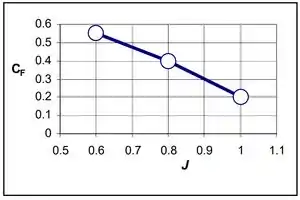
Passo 2
Neste caso vamos começar calculando :
Bem, vamos supor que para este valor de o valor é 0,1. Agora é só calcular , lembrando que a 4000m de altitude :