Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 13.Problemas - Ex. 90

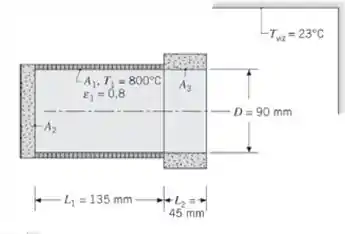
Um forno cilíndrico usado para o tratamento térmico de materiais no ambiente de uma nave espacial tem um diâmetro de 90 mm e um comprimento total de 180 mm. Os elementos aquecedores, na seção com 135 mm de comprimento (1), mantêm um revestimento refratário com ε1 = 0,8 a 800°C. Os revestimentos das seções inferior (2) e superior (3) são feitos com o mesmo material refratário, porém são termicamente isolados. Determine a potência exigida para manter as condições de operação do forno quando a vizinhança se encontra a 23°C.

Passo 1

Shooow galerinha !! Vamos que vamos ...

O problema nos pediu para achar a potência, ou seja, transferência de calor pelo forno, certo?

Vamos melhorar este desenho aqui, tudo bem?

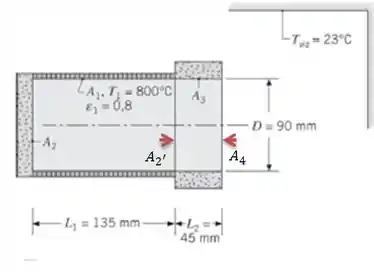
Isso vai ser importante lá na frente !!! Guardem no coração !

Para a taxa de radiação liquida transferida em uma superfície podemos usar a seguinte relação:

q i = E b i - J i 1 - ε i ε i A i = ∑ j = 1 4 J i - J j 1 A i F i j

Onde E b i é a potência emissiva, J i a radiosidade, A i a área e ε i a emissividade da superfície i.

Sabendo que para as superfícies (2) e (3) são isoladas termicamente:

q 2 = q 3 = 0

Vamos dar uma olhada nas equações abertas?

q 1 = E b 1 - J 1 1 - ε 1 ε 1 A 1 = J 1 - J 2 1 A 1 F 12 + J 1 - J 3 1 A 1 F 13 + J 1 - J 4 1 A 1 F 14

q 2 = 0 = J 2 - J 1 1 A 2 F 21 + J 2 - J 3 1 A 2 F 23 + J 2 - J 4 1 A 2 F 24

q 3 = 0 = J 3 - J 1 1 A 3 F 31 + J 3 - J 2 1 A 3 F 32 + J 3 - J 4 1 A 3 F 34

Já a superfície 4, o ambiente, por ser um recipiente grande no qual estão inseridos os objetos, ele irá se comportar como corpo negro, ou seja:

J 4 = E b 4 = σ T 4 4

Lembrando que:

σ = 5,67 × 10 - 8   W m 2 K 4

T 1 = 800 ° C + 273 = 1073   K

T 4 = 230 ° C + 273 = 296   K

Então:

J 4 = 5,67 × 10 - 8   W m 2 K 4 296   K 4 = 435,3   W m 2

Também podemos aproveitar e calcular a potência emissiva para a superfície 1:

E b 1 = 5,67 × 10 - 8   W m 2 K 4 1073   K 4 = 75159   W m 2

Nós também sabemos que:

ε 1 = 0,8

Então nós precisamos dos fatores de forma para conseguirmos calcular as radiosidades !!

Passo 2

Quanto aos fatores de forma nós podemos concluir por inspeção que:

F 22 = F 44 = 0

Para discos paralelos coaxiais nós podemos achar três fatores de forma, F 24 ,   F 22 ' e F 42 ' .

Começando por F 24 :

F 24 = 0,5   S - S 2 - 4 r 4 r 2 2 1 2

Lembrando que:

S = 1 + 1 + R 4 2 R 2 2

R 2 = r 2 L

R 4 = r 4 L

Sabendo que:

r 2 = r 4 = 45   m m

L = 180   m m

Então:

S = 1 + 1 + 45 180 2 45 180 2 = 18

Colocando no fator de forma:

F 24 = 0,5   18 - 18 2 - 4 45 45 2 1 2 = 0,0557

Para achar o fator forma F 22 ' nós usamos uma relação similar:

F 22 ' = 0,5   S - S 2 - 4 r 2 ' r 2 2 1 2

Onde:

S = 1 + 1 + R 2 ' 2 R 2 2

R 2 = r 2 ' L 1

R 2 = r 2 L 1

Lembrando que:

r 2 ' = r 2 = 45   m m

L 1 = 135   m m

Então:

S = 1 + 1 + 45 135 2 45 135 2 = 11

F 22 ' = 0,5   11 - 11 2 - 4 1 2 1 2 = 0,09167

E para F 42 ' nós usamos uma relação similar:

F 42 ' = 0,5   S - S 2 - 4 r 2 ' r 4 2 1 2

Onde:

S = 1 + 1 + R 2 ' 2 R 4 2

R 2 = r 2 ' L 2

R 4 = r 4 L 2

Lembrando que:

r 2 ' = r 2 = 45   m m

L 2 = 45   m m

Então:

S = 1 + 1 + 45 45 2 45 45 2 = 3

F 42 ' = 0,5   3 - 3 2 - 4 1 2 1 2 = 0,382

Passo 3

Ainda estamos longe de terminar, certo?

Agora nós vamos achar os fatores de forma usando a soma entre eles e a reciprocidade !!

Para a superfície A 2 :

F 21 = 1 - F 22 ' = 0,9083

Utilizando o teorema da reciprocidade:

F 12 A 1 = F 21 A 2

Se:

A 1 = π D L 1

A 2 = π D 2 4

Então:

F 12 = F 21 π D 2 4 π D L 1 = F 21 D 4 L 1

Substituindo:

F 12 = 0,9083 × 0,09   m 4 0,135   m = 0,1514

Pelo somatório para a superfície 1 podemos achar mais um fator de forma:

F 11 = 1 - F 12 - F 12 ' = 1 - 2 0,1514 = 0,6972

E agora para a superfície 4:

F 43 = 1 - F 42 ' - F 44 = 1 - 0,382 = 0,6180

Bom galerinha, nós ainda temos muitíssimos fatores de forma para achar, mas para não me estender aqui vocês podem fazer aí, basta usar a soma e a reciprocidade, e eu vou colocar os demais nesta tabela:

Passo 4

Agora nós vamos substituir tudo nas equações do Passo 1:

75159   - J 1 1 - 0,8 0,8 = J 1 - J 2 1 0,1514 + J 1 - J 3 1 0,097 + J 1 - 435,3 1 0,05438

0 = J 2 - J 1 1 0,9083 + J 2 - J 3 1 0,03597 + J 2 - 435,3 1 0,0557

0 = J 3 - J 1 1 0,2911 + J 3 - J 2 1 0,01798 + J 3 - 435,3 1 0,3090

Resolvendo as três equações simultaneamente:

J 1 = 73084 W m 2

J 2 = 67723 W m 2

J 3 = 36609 W m 2

Agora podemos calcular a potência, basta lembrarmos que:

q 1 = 75159   - 73084 1 - 0,8 0,8 π 0,90 0,135 = 317   W

Bem grandinha não foi pessoal ?? MAS respirem fundo que com calma vocês vão entender !!

Resposta

q 1 = 317   W

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Considere uma superfície cilíndrica e um disco orientado coaxialmente, como mostrado na Fig. 13-19. O cilindro tem um diâmetro D e um comprimento L. O disco de diâmetro D é colocado coaxialmente com o
Determine os quatro fatores de formas associados a um recinto formado por dois cilindros concêntricos muito longos de raios r 1er 2 . Despreze os efeitos das extremidades.
Determine o fator de forma a partir da base de um cubo para cada uma das outras cinco superfícies.
Determine o fator de forma das ranhuras muito longas mostradas na Fig. P13–17 para o lado externo, sem usar tabelas ou gráficos de fatores de forma. Despreze os efeitos das extremidades.
Determine o fator de forma F 12 entre as superfícies retangulares mostradas na Fig. P13–15.