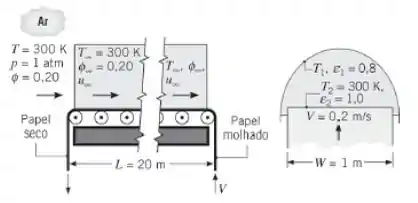
Um forno radiante para a secagem de papel de impressão é constituído por um longo duto (L = 20 m) com seção transversal semicircular. O papel se move ao longo do forno sobre uma esteira transportadora a uma velocidade de V = 0,2 m/s. O papel tem um teor de água de 0,02 kg/m² quando entra no forno e encontra-se completamente seco ao sair do forno. Para assegurar qualidade, o papel deve ser mantido à temperatura ambiente (300 K) durante sua secagem. Para auxiliar na manutenção dessa condição, todos os componentes do sistema e o ar que escoa através do forno estão a uma temperatura de 300 K. A superfície interna do duto

semicircular, que tem uma emissividade de 0,8 e uma temperatura T1, fornece o calor radiante necessário para proceder à secagem. A superfície molhada do papel pode ser considerada negra. O ar que entra no forno encontra-se a uma temperatura de 300 K, com umidade relativa de 20%. Como a velocidade do ar é elevada, sua temperatura e umidade relativa

podem ser consideradas constantes ao longo de todo o comprimento do forno. Calcule a taxa de evaporação exigida, a velocidade do ar , e a temperatura T1 que irão assegurar ao processo condições de regime estacionário.

Bom, agora nós queremos achar a velocidade do ar ! E aqui nós temos uma fórmula também bastante conhecida!!

Quem aí lembra do Reynolds?

Onde:

Então:

Nós sabemos que:

Ainda não temos as propriedades, não é?

Então vamos aproveitar e olhar todos os dados que vamos precisar, lembrando que a temperatura é de 300 K.

Olhando na Tabela A – 4, para o ar:

Na Tabela A – 6, para o vapor de água:

Na Tabela A – 8, para o vapor de água e ar:

Até chegar no Reynolds nós termos um trabalhinho !!

Primeiro vamos usar a relação para o fluxo mássico:

O problema nos deu que:

Então:

Mas ainda não achamos o que precisávamos !! Só que com o coeficiente nós podemos achar o número de Schmidt:

E este número também pode ser escrita ao longo do comprimento do forno:

Agora sim, vamos substituir:

Resolvendo:

Bom galerinha, este ainda não é o Reynolds que queremos, porque ele só vai nos dar um indício das características do fluxo para a corrente livre no fluido!

Como nós podemos usar a seguinte relação para o novo Reynolds:

Substituindo:

E agora sim:

Agora nós só precisamos achar uma coisinha, não é?

Nós queremos achar agora a temperatura !!

Como o calor que estão sendo usado para evaporar o líquido é fornecida por radiação:

O calor por radiação é dado por:

Então, para duas superfícies

Já sabemos que:

A área da seção transversal semicircular é dada por:

Pela reciprocidade:

Substituindo:

Ufaaa !! Acabamos !!