Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 8º - Capítulo 13.Problemas - Ex. 49
Um forno tem a forma de uma seção de cone truncado, como mostrado na figura. O piso do forno tem uma emissividade de e é mantido a com um fluxo térmico de . A parede lateral é isolada termicamente e tem uma emissividade de . Considere que todas as superfícies sejam difusas e cinzas.
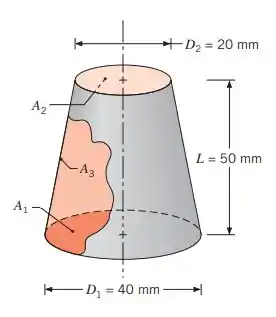
(a) Determine a temperatura da superfície superior, , se sua emissividade for igual a . Qual é a temperatura da parede lateral, ?
(b) Se as condições no piso do forno permanecerem as mesmas, mas todas as superfícies forem negras ao invés de difusas e cinzas, determine e . A partir da análise das cavidades difusas e com comportamento de corpo negro, o que você pode dizer sobre a influência de ε2 em seus resultados?
Passo 1
E aí, tudo bem?
Vem comigo na resolução dessa questão!
Começamos o nosso problema realizando balanços de energia para as três superfícies do invólucro para encontrarmos suas radiosidade.
- Superfície 1:
- Superfície 2:
- Superfície 3:
Onde os poderes emissivos do corpo negro são da forma:
E
Passo 2
Calculando a radiação líquida que deixa :
Também podemos escrever da seguinte forma:
Substituindo os dados:
Sendo a superfície lateral adiabática:
A partir da qual reconhecemos , mas descobriremos isso como um resultado da nossa análise.
Para o gabinete, , há fatores de visualização, para os quais deve ser determinado diretamente.
Os valores de foram obtidos por meio de softwares recomendados:
Passo 3
Para as relações propostas anteriormente, podemos determinar e .
As temperaturas e serão avaliadas a partir da relação .
Utilizando o auxílio de softwares recomendados, aplicando as relações nele, obtemos para as letras (a) e (b) os seguintes resultados:
Até a próxima questão!