Fornos isotérmicos com pequenas aberturas, que se aproximam de um corpo negro, são usados com frequência para calibrar medidores de fluxo térmico, termômetros de radiação e outros equipamentos radiométricos. Em tais aplicações, é necessário controlar a potência que é fornecida ao forno, de tal maneira que a variação da temperatura e da intensidade espectral da abertura fique dentro de limites desejáveis.
- Levando em consideração a distribuição espectral de Planck, Equação 12.30, mostre que a razão entre a variação relativa da intensidade espectral e a variação relativa da temperatura do forno tem a forma
- Usando essa relação, determine a variação permissível na temperatura do forno, operando a 2000 K, para garantir que a intensidade espectral a 0,65 μm não irá variar em mais de 0,5%. Qual é a variação permissível para 10 μm?
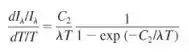
Passo 1
Temos duas letrinhas para resolver! Vamos lá!
Começando pela letra a, precisamos fazer uma demonstração, certo?
Vamos primeiro escrever a equação 12.30:
Se a gente fizer o logaritmo natural nos dois lados teremos o seguinte:
Agora vamos fazer a derivada dele, lembrando que é uma constante, beleza?
E fazendo a razão ficaremos com:
ou
Show de bola! Partiu letra b!
Passo 2
Agora vamos encontrar a variação da temperatura no forno, beleza?
Considerando um , um e um , vamos ter:
Então nossa variação de temperatura vai ser:
Passo 3
Ainda na letra b, vamos considerar agora um , ficaremos com:
E a nova variação de temperatura será:
Show! Arrasamos!
Resposta
- Passo 1.
- Para :
Para :