Uma função corrente para um escoamento plano, irrotacional, em coordenadas polares é
Encontre o potencial de velocidade para esse escoamento. Faça o esboço de algumas linhas de corrente e linhas equipotenciais e interprete o padrão de escoamento.
Passo 1
Bora pra mais uma!
Vamos encontrar o potencial de velocidade:
Integrando ambas as equações e as comparando obtemos:
Resposta
O perfil das linhas de corrente e equipotenciais deste caso, se assemelha a um tornado, conforme esboço abaixo:
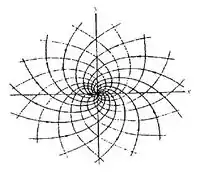
E o potencial de velocidade para este escoamento é dado pela equação