Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 3.Problemas - Ex. 67

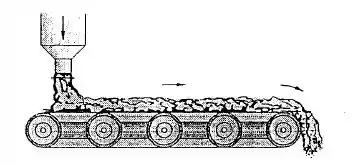
Um funil de carga descarrega cascalho à taxa de 650 N/s sobre uma correia transportadora como mostra abaixo. Em seguida o cascalho é transportado até o final da correia. As rodas de acionamento têm 80 cm de diâmetro e giram no sentido horário de 150 rpm. Desprezando o atrito do sistema e o arrasto do ar, calcule a potência requerida para acionar essa correia.

Passo 1

E aí, galera!! Tranquilidade por aí? Hoje eu vim aqui pra te ensinar como podemos resolver esse problema aí de cima :D

Primeiro de tudo, bora colocar um volume de controle nesse problema!!!

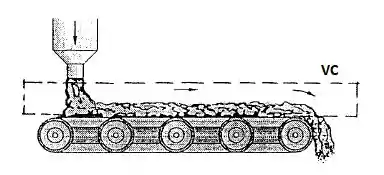
O problema está pedindo para calcularmos a potência requerida, ou seja, P = F c o r r e i a V c o r r e i a

Passo 2

Bem, a velocidade da correia será dada pelo produto de sua velocidade angular com o raio das rodas, ou seja, temos:

V c o r r e i a = V s a í d a = Ω R r o d a = 150   r e v m i n x   2 π   r a d r e v 1 m i n 60 s = 6,28   m / s

Passo 3

A correria aplica uma força tangencial ao funil. Com isso podemos escrever que nosso balanço de forças será dado na direção x tal que:

∑ F x = F c o r r e i a = m ˙ s u s - m ˙ e u e

A gente sabe qual é nossa vazão em peso de saída, certo? Mas aqui eu quero te chamar atenção para uma coisa, você vai perceber que olhando para nosso volume de controle, nós temos que a velocidade de entrada é zero!

F c o r r e i a = m ˙ s u s = m ˙ s V s a í d a

O enunciado deu pra gente a vazão em peso, então precisamos transformar ela em vazão mássica para obtermos as unidades coerentes entre si, show?

m ˙ s = P ˙ g = 650 9,81 = 66,26   k g / s

Substituindo na nossa equação, teremos que F c o r r e i a = 66,26   x   6,28 = 416   N

Passo 4

Agora que conhecemos a velocidade da correia e também a sua força, podemos calcular a potência requerida, certo?

P = F c o r r e i a V c o r r e i a = 416   x   6,28 = 2600   W

Resposta

P = 2600   W

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um aspersor de jardim com três braços idênticos é usado para molhar um jardim, girando cm um plano horizontal pelo impulso causado pelo escoamento da água. A água entra no aspersor ao longo do eixo de
A água escoa e é descarregada de uma seção de tubo em U, como mostra a Figura . No flange (1), a pressão absoluta total é 200 kPa e 30 kg/s escoam para dentro do tubo. Noflange (2), a pressão total é
A água escoa através de um tubo com 12 cm de diâmetro que consiste em uma seção vertical com 3 m de comprimento e horizontal com 2 cm de diâmetro com um cotovelo de 90° na saída para forçar a água a s
Uma cunha divide uma lâmina de água a 20°C, como mostra abaixo. Tanto a cunha quanto a lâmina de água são muito longas na direção normal ao papel. Se a força necessária para manter a cunha estacionári
Um jato líquido de velocidade V j e diâmetro D j atinge um cone oco e fixo, como na figura abaixo, sendo defletido de volta, na forma de uma camada cônica de mesma velocidade. Encontre o ângulo do con