Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 3.Problemas - Ex. 51

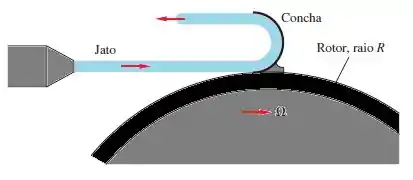
Um jato líquido com velocidade V j e área A j atinge uma única concha do rotor de uma turbina girando com velocidade angular Ω . Deduza uma expressão para a potência P fornecida pelo rotor nesse instante, em função dos parâmetros do sistema. Para qual velocidade angular ocorre a máxima potência fornecida? Como sua análise mudaria se houvesse muitas e muitas conchas no rotor de modo que o jato fosse atingindo continuamente pelo menos uma concha?

Passo 1

MEU DEUS ESSA QUESTÃO PARECE SER MUITO DIFÍCILLLLL!!!!

Calmaaaa, galera! Vem comigo que é sucesso!

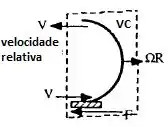
Primeiro de tudo vamos fazer um volume de controle e vamos dizer que a velocidade do jato será dada por V = Ω R , isso nos diz que o jato entrará no volume de controle com uma velocidade relativa de V j - Ω R

Passo 2

Pelo balanço de forças, a gente vai ter o seguinte:

∑ F x = - F c o n c h a = m ˙ s u s - m ˙ e u e

Como temos um fluido incompressível, as vazões devem ser iguais!!

∑ F x = - F c o n c h a = m ˙ u s - u e = m ˙ - V j - Ω R - V j - Ω R

F c o n c h a = 2 m ˙ V j - Ω R = 2 ρ A j V j - Ω R 2

Passo 3

A potência pode ser dada pela equação: P = Ω R F c o n c h a = 2 ρ A j Ω R V j - Ω R 2

E a potência máxima pode ser calculada quando derivamos P em função da velocidade angular e igualamos a zero!!

d P d Ω = 0

Obtemos que   Ω R = V j 3 , substituindo na nossa equação de P:

P = 2 ρ A j V j 3 V j - V j 3 2 = 2 ρ A j V j 3 2 V j 3 2 → P m á x = 2 ρ A j V j 3 4 V j 2 9 = 8 27 ρ A j V j 3

Passo 4

Se houvessem muitas conchas, poderíamos ter que a vazão mássica disponível seria dada por:

m ˙ d i s p o n í v e l = ρ A j V j

Já vimos que: P = 2 ρ A j V j Ω R V j - Ω R

Fazendo o mesmo procedimento do passo 3, teríamos que P m á x = 1 2 ρ A j V j 3 para Ω R = V j 2

Resposta

P m á x = 2 ρ A j V j 3 4 V j 2 9 = 8 27 ρ A j V j 3

P m á x = 1 2 ρ A j V j 3

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma patinadora de 60k g está de pé sobre o gelo com patins (atrito desprezível). Ela segura uma mangueira flexível (essencialmente sem peso) que direciona uma corrente de água com 2c m de diâmetro e p
Trilhos de guia vertical quase sem atrito mantêm uma placa de massa m p em posição horizontal, de forma que ela possa deslizar livremente na direção vertical. Um bocal direciona uma corrente de água d
Indiana Jones precisa subir em um prédio de 10m de altura. Existe uma mangueira grande cheia com água pressurizada pendurada no alto de prédio. Ele constrói uma plataforma quadrada e monta quatro boca
Reconsidere o Problema 6-26. Se a massa do carrinho for 300k g e os freios falharem, determine a aceleração do carrinho quando a água atingi-lo pela primeira vez. Suponha que a massa da água que molha
Mostre que a força exercida por um jato de líquido em um bocal fixo quando ele sai com uma velocidade V é proporcional a V 2 ou, altenativamente, a m ˙ 2 .