Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 8º - Capítulo 2.Problemas - Ex. 62

Gate AB in Fig. P2.62 is 15 ft long and 8 ft wide into the

paper and is hinged at B with a stop at A. The water is at

208C. The gate is 1-in-thick steel, SG 5 7.85. Compute the

water level h for which the gate will start to fall

Passo 1

Saaaalve, tranquilo? Vamos lá resolver mais uma questão juntos?! 😊

Os dados são os seguintes:

Comprimento do portão: L = 15 f t

Largura do portão: b = 8 f t

Espessura do portão: t = 1   i n = 1 12 f t Gravidade específica do portão: S G = 7.85 Massa da carga, Comentários: m = 10000 l b

Passo 2

Peso do portão, volume do portão

W = S G × γ water  × volume do portão

  = 7.85 × 62.4 × 15 × 8 × 1 12   = 4898.4 l b f

O comprimento do portão encontra-se na água,

l = h s i n ⁡ 60 ∘

l = 1.1547   h

A área da porção do portão encontra-se na água,

A = h s i n ⁡ 60 ∘ × b

  = h 0.866 × 8   = 9.2376   h

Somente esta parte contribui com força hidrostática.

Passo 3

Distância centríodal da superfície da água

h ‾ = h 2

h ‾ = 0.5 h Força hidrostática,

F = γ á gua   A h ‾

  = 62.4 × 9.2376   h × h 2   = 288.21   h 2

Passo 4

Desenhe o diagrama de corpo livre do portão da seguinte forma:

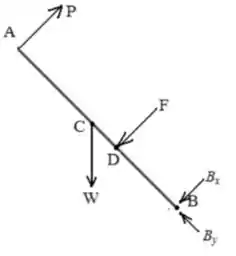
Passo 5

Momento de inércia da porta,

I G = b l 3 12

= 8 × ( 1.1547 h ) 3 12 = 1.0264 h 3

Linha de ação da força hidrostática,

B D = l 2 - I G s i n ⁡ 60 ∘ A h ‾ = 1.1547 h 2 - 1.0264 h 3 × s i n ⁡ 60 ∘ 9.2376   h × 0.5   h = ( 0.57735   h - 0.19245   h ) = 0.3849   h

Passo 6

Tomando impulso sobre B, ∑ M B = 0

P × A B - W × B C - F × B D   = 0 ( 10000 × 15 ) - 4898.4 × 7.5 c o s ⁡ 60 ∘ - 288.21 h 2 × 0.3849 h = 0 131631 - 110.932 h 3   = 0 h 3   = 131631 110.932 h   = 1186.6 3   = 10.587

Portanto, o nível da água h é 10.587   m .

Resposta

h = 10.587

Exercícios de Livros Relacionados

Generalizando o problema P2.66 da seguinte maneira: represente a distancia AB por H, a distância BC por L e o ângulo ABC por θ . Considere que o material da barragem tenha densidade d. A largura da ba
Para o cilindro semicircular CDE no Exemplo 2.9, encontre a força hidrostática vertical integrando o componente vertical da pressão sobre a superfície de θ = 0 até θ = π .
Uma barragem de concreto (d = 2,5) é construída na forma de um triângulo isósceles, como na Figura P2.80. Analise essa geometria para encontrar o intervalo de ângulos θ para o qual a força hidrostátic
A barragem na Figura P2.82 é um quarto de círculo com largura de 50 m. Determine os componentes horizontal e vertical da força hidrostática contra a barragem e o ponto CP em que a resultante atinge a
A comporta AB na Figura P2.83 é um quarto de círculo de 3 m de largura, articulada em B. Encontre a força F suficiente apenas para impedir que a comporta se abra. A comporta é uniforme e pesa 13.350 N