Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 8º - Capítulo 13.Problemas - Ex. 102

Um novo equipamento de reciclagem por infravermelho foi proposto para reciclar os milhões de quilos de plásticos descartados pelo desmonte e prensagem de veículos automotivos após sua “aposentadoria”. Para atacar o problema de classificar plásticos misturados em componentes como polipropilenos e policarbonatos, uma corrente lavada de plásticos misturados é direcionada para um sistema de aquecimento por infravermelho, no qual ela é seca e posteriormente aquecida a uma temperatura na qual um dos componentes começa a amolecer, enquanto os outros permanecem rígidos. A corrente misturada é então passada através de rolos de aço, aos quais o plástico amolecido se adere, sendo então removido da corrente. O aquecimento da corrente é então continuado para facilitar a remoção de um segundo componente e o processo de aquecimento/remoção é repetido até que todos os componentes sejam separados.

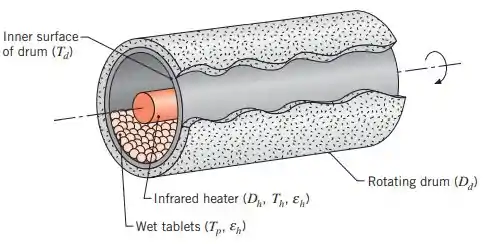
Considere o estágio inicial da secagem em um sistema composto por um aquecedor cilíndrico alinhado coaxialmente com um tambor rotativo de diâmetro D d = 1   m . Logo após entrar no tambor, os pellets de plástico úmidos podem ser considerados cobrindo toda a seção semicilíndrica inferior e permanecendo a uma temperatura de T p = 32 5   K durante o processo de secagem. A área da superfície dos pellets pode ser suposta igual à do semicilindro e sua emissividade é de ε p = 0,95 .

(a) Se o escoamento do ar seco através do tambor mantém um coeficiente de transferência de massa convectiva de 0,02 4   m / s na superfície dos pellets, qual é a taxa de evaporação por unidade de comprimento do tambor?

(b) Desprezando a transferência de calor por convecção, determine a temperatura T a que tem que ser mantida por um aquecedor com diâmetro D a = 0,10   m e emissividade ε a = 0,8 para sustentar a taxa de evaporação anterior. Qual é o valor correspondente da temperatura T d da superfície superior do tambor? A superfície externa do tambor é isolada termicamente e a razão comprimento/diâmetro do tambor é grande. Podendo ser aplicado às superfícies do topo ( d ) ou da base ( p ) do tambor, o fator de forma de um semicilindro infinitamente longo para si próprio, na presença de um cilindro coaxial concêntrico (diâmetro D h ), pode ser calculado por

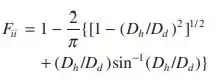
Passo 1

Começamos o nosso problema obtendo algumas propriedades para a água saturada a 32 5   K na Tabela A.6:

ρ s a t = 1 v g = 1 11,09 = 0,0 904   k g / m 3

h h f g = 23 78 × 10 3   J / k g

Vamos aos cálculos!

Passo 2

Letra a)

Calculando a taxa de evaporação por unidade de comprimento do tambor:

m ˙ ' = h m A s ρ s a t , T p - ρ s a t , T ∞

Sendo:

A s = π D d 2 = π ⋅ 1 2 = π 2   m

E como não temos água no exterior:

ρ s a t , T ∞ = 0

Substituindo os dados:

m ˙ ' = 0,02 4 ⋅ π 2 ⋅ 0,0 904 - 0

m ˙ ' = 0,00341   k g / m ⋅ s

Bora para a letra (b)!

Passo 3

Letra b)

Aqui, queremos T a e T d , então vamos encontra-los!

Como não possuímos convecção, somente a radiação está fornecendo calor suficiente para evaporar a água:

q r a d ' = q e v a p ' = m ˙ ' h f g

Temos que a transferência de calor por radiação também pode ser dada por:

σ T a 4 - T p 4 1 - ε a ε a A a ' + 1 A a ' F a p + 1 A a ' F a d + 1 A p ' F p d - 1 + 1 - ε p ε p A p ' = m ˙ ' h f g

Onde:

A a ' = π D a = 0,1 π = 0,314   m

A p ' = π D d 2 = 0 , 5 π = 1,57   m

Em relação aos fatores de forma podemos inferir que:

F a p = F a d = 0,5

Por reciprocidade:

F p a A p ' = F a p A a '

F p a = A a A p ⋅ F a p = 0,314 1,57 ⋅ 0,5 = 0,1

O problema nos disse como calcular F p p :

F p p = 1 - 2 π 1 - D a D d 2 1 2 + D a D d ⋅ sin - 1 ⁡ D a D d

Substituindo os dados:

F p p = 1 - 2 π 1 - 0,1 1 2 1 2 + 0,1 1 ⋅ sin - 1 ⁡ 0,1 1

F p p = 0,36

Utilizando o somatório para a superfície p :

F p d + F p a + F p p = 1

F p d + 0,1 + 0,36 = 1

F p d = 0,54

Substituindo os dados na nossa equação:

5,67 × 10 - 8 ⋅ T a 4 - 32 5 4 1 - 0,8 0,8 ⋅ 0,314 + 1 0,314 ⋅ 0,5 + 1 0,314 ⋅ 0,5 + 1 1,57 ⋅ 0,54 - 1 + 1 - 0,95 0,95 ⋅ 1,57 = 0,00341 ⋅ 2378 × 10 3

T a = 889   K

Passo 4

Para encontrarmos T d , utilizaremos o fluxo de transferência de calor da vizinhança para o aquecedor:

q = σ T a 4 - J a 1 - ε a ε a A a ' = m ˙ ' h f g

Calculando J a :

5,67 × 10 - 8 ⋅ 889 4 - J a 1 - 0 , 8 0,8 ⋅ 0,314 = 0,00341 ⋅ 23 78 × 10 3

J a = 28920   W / m 2

Fazendo um balanço de energia para a vizinhança:

J a - J d 1 A a ' F a d - J d - J p 1 A p F p d = 0

Abrindo essa equação:

J a - σ T d 4 1 A a ' F a d - σ T d 4 - T p 4 1 A p F p d = 0

Substituindo os dados:

28920 - 5,67 × 10 - 8 ⋅ T d 4 1 0,314 ⋅ 0,5 - 5,67 × 10 - 8 ⋅ T d 4 - 325 4 1 1,57 ⋅ 0,54 = 0

Resolvendo essa equação, obtemos:

T d = 811   K

Até a próxima questão!

Resposta

a )   m ˙ ' = 0,00341   k g / m ⋅ s

b )   T a = 889   K ;   T d = 811   K

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma liga de alumínio fundida a 900 K é despejada em um recipiente cilíndrico que é isolado termicamente de uma grande vizinhança a 300 K. O diâmetro interno do recipiente é de 250 mm e a distância do
A relação de reciprocidade, a regra da soma e as Equações 13.5 a 13.7 podem ser usadas para desenvolver relações para o fator de forma que permitem a utilização das Figuras 13.4 e/ou 13.6 para configu
Dois discos planos coaxiais estão separados por uma distância L = 0 , 8 0m . O disco inferior ( A 1 ) é sólido e tem um diâmetro D e = 0,80m e uma temperatura T 1 = 300K . O disco superior ( A 2 ) , a
Um orifício com fundo plano e 8m m de diâmetro é perfurado até uma profundidade de 24m m em um material cinza e difuso, que tem uma emissividade de 0,8 e uma temperatura uniforme de 1000K .(a) Determi
Considere uma janela de vidro duplo. A superfície do vidro pode ser tratada com um revestimento de baixa emissividade para reduzir sua emissividade de ε = 0,95 para ε = 0,05 . Determine o fluxo térmic