Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 8º - Capítulo 1.Problemas - Ex. 40
Glycerin at 208C fills the space between a hollow sleeve of
diameter 12 cm and a fi xed coaxial solid rod of diameter
11.8 cm. The outer sleeve is rotated at 120 rev/min.
Assuming no temperature change, estimate the torque required, in N · m per meter of rod length, to hold the inner
rod fixed.
Passo 1
Saaaalve, tranquilo? Vamos lá resolver mais uma questão juntos?! 😊
Considerando o seguinte diagrama que representa o perfil de velocidade em um espaço anelar
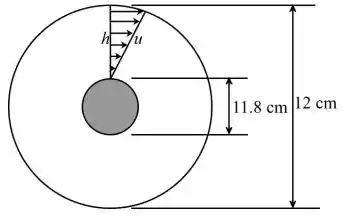
Passo 2
Obtendo a viscosidade dinâmica da glicerina à
Considerando que a parte externa rotaciona a uma velocidade de
Calculando a velocidade angular
Aqui, a velocidade do cilindro é
Substituindo os valores
Passo 3
Calculando a velocidade linear da roda usando
Aqui, a velocidade linear é e o diâmetro é
Substituindo valores
Passo 4
Calculando a distancia entre as rodas
onde, é o diâmetro oco
Substituindo valores
Passo 5
Calculando a tensão de cisalhamento na glicerina usando
Aqui, é a tensão de cisalhamento desenvolvida na glicerina e é a viscosidade dinâmica da glicerina
Substituindo valores
Passo 6
Calculando a força de cisalhamento agindo paralelamente à roda da superfície
Aqui, é a força cisalhante e é a área da superfície
Substituindo valores
Passo 7
O cilindro interno rotaciona à respeito da rotação da manga, devido à tensão cisalhante induzida na parte de glicerina.
A força cisalhante agindo na manga é igual a força cisalhante agindo no cilindro interno.
Para fazer o cilindro interno rígido, temos que aplicar um torque contrário ao cilindro interno.
Calculando o torque por unidade de comprimento necessário para segurar a manga interna rígida:
Aqui, é o torque por unidade de comprimento e é o raio da roda interna
Substituindo valores