Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 9.Problemas - Ex. 121

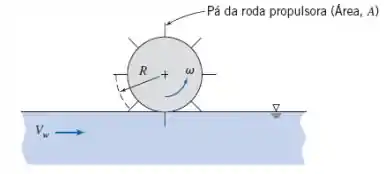
Uma grande roda de pás está imersa na correnteza de um rio para gerar potência. Cada pá tem área A e coeficiente de arrasto C A ; o centro de cada pá está localizado no raio R a partir da linha de centro da roda. Considere que o equivalente a uma pá está continuamente submerso na corrente de água. Obtenha uma expressão para a força de arrasto sobre uma única pá em termos das variáveis geométricas, velocidade da correnteza, V, e velocidade linear do centro da pá, U = Rμ. Desenvolva expressões para o torque e a potência produzidos pela roda. Determine a velocidade na qual a roda de pás deveria girar para dar a máxima produção de potência em uma dada correnteza.

Passo 1

Fala aí galera, vamos para mais um problema de mecânica dos fluidos. Primeiro, sabemos que:

F A = 1 2 ρ A V 2 C A

T = F A R

P = T ω

Sabemos que a velocidade relativa é:

V r e l = V - U = V - R ω

Logo:

F A = C A A 1 2 ρ V - U 2

Já o torque, será:

T = F A R = C A A 1 2 ρ V - U 2 R

A potência será:

P = T ω = C A A 1 2 ρ V - U 2 R ω = C A A 1 2 ρ V - U 2 U

Logo, para otimizar a potência:

d P d U = C A A 1 2 ρ 2 V - U U - 1 + V - U 2 = 0

Cancelando o fator V - U ,   teremos:

- 2 U + V - U = 0

V - 3 U = 0

U = R ω = V 3

Logo:

ω o t i m o = V 3 R

Resposta

ω o t i m o = V 3 R

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um arremessador (pitcher) de beisebol arremessa uma “bola com efeito” à velocidade inicial de 105 km/h e uma rotação de 6.500 rpm em torno de um eixo vertical. Uma bola de beisebol pesa 1,42 N e tem u
Uma bola de tênis de mesa tem massa de 2,6 g e diâmetro de 3,81 cm. A bola será golpeada horizontalmente a uma velocidade inicial de 20 m/s quando estiver a 50 cm acima da mesa, como na Figura P7.111.
Seja um avião de peso P , área de asa A , razão de aspecto R A , voando a uma altitude em que a massa específica é ρ . Admita que todo o arrasto e toda a sustentação se devam à asa, que tem um coefici
Uma asa de 2 % de arqueamento, 127m m de corda e 762m m de envergadura é testada com um certo ângulo de ataque em um túnel de vento com ar em condições padrão ao nível do mar a 61m / s , medindo-se um
O avião Boeing 727 tem um peso global de 556.000N , uma área de asa de 111,5m 2 e uma razão de aspecto de 6 . É equipado com dois motores turbofan e voa a 856k m / h a9.100m de altitude padrão. Admita