Um helicóptero sem car ga de massa flutua ao nível do mar enquanto é carregado. No modo de flutuação sem carga, as pás giram a . As pás horizontais acima do helicóptero fazem com que uma massa de ar de de diâmetro se mova para baixo a uma velocidade média proporcional à velocidade rotacional geral da lâmina (rpm). Uma carga de é carregada no helicóptero e o helicóptero se eleva lentamente. Determine (a) a inversão da vazão de ar volumétrico que o helicóptero gera durante a flutuação sem carga e a entrada de potência necessária e (b) a rpm das pás do helicóptero para flutuar com a carga de e a entrada de potência necessária. Tome a densidade do ar atmosférico . Suponha que o ar se aproxime das pás pelo alto através de uma área grande com velocidade desprezível, e que o ar seja forçado pelas pás a se mover para baixo com velocidade uniforme através de um cilindro imaginário cuja base é a área de envergadura da pá.
Passo 1
O enunciado quer saber primeiro a vazão mássica de ar que as pás do helicóptero sem carga produzem e a potência que o helicóptero sem carga precisa produzir para se sustentar no ar. O primeiro passo para calcular essas duas incógnitas é escolher um volume de controle. Como queremos informações sobre o helicóptero, escolheremos um volume de controle em forma de cilindro de diâmetro que engloba o helicóptero.
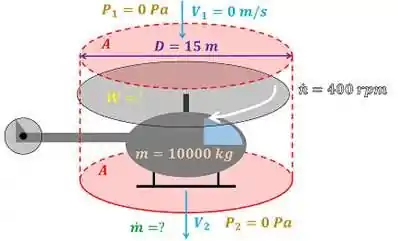
é a envergadura das pás do helicóptero. é a área através da qual o escoamento de ar passa. é a velocidade de rotação das pás do helicóptero em . é a massa presente no volume de controle. Quando o helicópterio está sem carga, é apenas a massa do helicóptero. é a velocidade do ar entrando no volume de controle. Ela é desprzível. Logo:
é a velocidade do ar saindo do volume de controle. e são as pressões manométricas do ar entrando e saindo do volume de controle respectivamente. Elas valem zero, porque essas pressões são iguais às pressões atmosféricas.
No próximo passo vamos aprender a calcular o que a questão pede.
Passo 2
Para encontrar vazão precisamos aplicar a segunda lei de Newton (equação da quantidade de movimento) ao volume de controle. Podemos considerar que o escoamento de ar ocorre em regime permanente, porque as turbina geralmente operam dessa forma. Como estamos interessados apenas na velocidade vertical (eixo ), adaptamosa equação do livro (segunda lei de Newton no eixo para volumes de controle em regime permanente).
onde é o somatório das forças verticais (no eixo ) sobre o volume de controle, é o fator de correção para o escoamento que entra no volume de controle. é o fator de correção para o escoamento que sai do volume de controle. Esses dois fatores de conversão valem , porque esse é o valor do fator de correção para escoamentos livres na atmosfera.
é a velocidade do ar no eixo entrando no volume de controle. Ela vale zero, porque é desprezível. é a velocidade do ar no eixo saindo do volume de controle. Ela é igual à velocidade , porque é uma velocidade vertical com o sentido de cima pra baixo.
A fórmula de pode ser simplificada se considerarmos o escoamento de ar incompressível (densidade do ar constante e igual a ).
Como a área pela qual o ar passa é circular, calculamos ela com a fórmula abaixo.
Logo:
Substituindo essas informações na fórmula de , encontramos:
A única força do eixo é a força peso do volume de controle. A força que a pressão atmosférica exerce sobre o volume de controle não é contabilizada, porque é atua sobre todo o volume de controle e seu efeito acaba sendo cancelado.
Substituindo isso na equação anterior de , encontramos:
Substituindo isso na fórmula de , achamos:
Passo 3
Para encontrar a potência que o helicóptero sem carga precisa produzir para se sustentar no ar, precisamos aplicar a primeira do no volume de controle.
onde é a altitude do ar entrando no volume de controle e é a altitude do ar saindo do volume de controle. Como a diferença entre essas duas altitudes é desprezível, podemos cortar e da equação.
Passo 4
Substituindo os dados na equação de , encontramos seu valor.
Substituindo os dados na equação de , também encontramos seu valor.
Passo 5
Depois de calcular esses valores, o enunciado pede que a gente calcule o valor da rotação das pás em , quando o helicóptero está carregado. Para calcular isso, temos que lembrar que a questão nos informou que a velocidade média é proporcional à velocidade rotacional geral da lâmina (rpm). Ou seja, é igual à multiplicação entre uma constante e .
A equação acima mostra que para encontrar , temos que achar . Achamos substituindo os valores de e para o caso no qual o helicóptero está sem carga.
Agora podemos encontrar a rotação , substituindo a fórmula de velocidade . No entanto, temos que lembrar que a velocidade mudará, quando o helicóptero passar a ter uma carga. Isso acontece, porque a massa do volume de controle deixa de ser só a massa do helicóptero e passa a ser a soma entre a massa do helicóptero e da carga. Logo:
Passo 6
Para encontrar substituímos os dados na mesma fórmula de que encontramos anteriormente. No entanto, tenha em mente que a massa do volume de controle aumenta!