Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 14.Problemas - Ex. 51
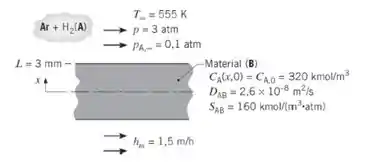
Hidrogênio gasoso é usado em um processo para fabricar uma folha de material com 6 mm de espessura. No final do processo, H2 permanece em solução no interior do material com uma concentração uniforme de 320 kmol/m3. Para remover o H2 do material, as duas superfícies da folha são expostas a uma corrente de ar a 500 K e a uma pressão total de 3 atm. Devido à contaminação, a pressão parcial de hidrogênio é de 0,1 atm na corrente de ar, que fornece um coeficiente de transferência de massa por convecção de 1,5 m/h. A difusividade mássica e a solubilidade do hidrogênio (A) no material (B) são DAB = 2,6 x 10−8 m2/s e SAB = 160
kmol/(m3 · atm), respectivamente.
- Se o material for deixado exposto à corrente de ar por um longo tempo, determine a quantidade final de hidrogênio no material (kg/m3).
- Identifique e estime o parâmetro que pode ser usado para determinar se o processo de difusão mássica transiente na folha pode ser considerado caracterizado por uma concentração uniforme em qualquer tempo durante o processo. Sugestão: Essa situação é análoga àquela usada para determinar a validade do método da capacitância global para a análise da transferência de calor transiente.
- Determine o tempo necessário para reduzir a concentração mássica do hidrogênio no centro da folha para o dobro do valor-limite calculado na parte (a).
Passo 1
Shoow de bolinhas galeraa ?! Vamos continuar?
Bom, o problema nos pediu na letra (a) para determinar a quantidade final de hidrogênio no material (kg/m³), ok?
O conteúdo final de hidrogênio no material da folha pode ser escrito como:
A massa molar do hidrogênio nós já sabemos:
Para achar a concentração no ambiente:
Onde:
Substituindo para achar a concentração:
Sendo assim:
E assim nós finalizamos a letra (a) !!
Passo 2
Bom, na letra (b) nós vamos começar escrevendo o fluxo difusivo dentro do material:
Onde é a difusividade mássica do hidrogênio no material da folha, é a concentração molar inicial do hidrogênio, a concentração molar final de hidrogênio e L a espessura do material da folha !!
Quando nós teremos o fluxo convectivo da espécie, e a fórmula é análoga a transferência de calor:
Onde é o coeficiente de transferência de massa convectiva, a concentração molar da espécie na superfície do matéria e a concentração no ar!!
Lembrando da lei dos gases ideais:
Então:
Manipulando a equação:
Como vimos na relação do Passo 1:
Onde é igual a !!
Passo 3
Agora que nós achamos estas duas equações nós vamos igualar:
Então:
O termo no numerador é referente a resistência a difusão, enquanto o denominador é referente a resistência a convecção:
Se vocês se lembram bem da definição do número de Biot:
Então:
Sabendo que:
Então:
Como a concentração pode ser considerada uniforme no material da folha, tudo bem até aqui?
Passo 4
Como nós estamos tratando o processo como concentração uniforme, podemos fazer a conservação as espécies no material:
O termo nós ainda não vimos, mas ele é descrito por:
Então:
Integrando:
E assim nós achamos o parâmetro necessário !!
Passo 5
Na letra (c) queremos achar o tempo necessário para reduzir a concentração mássica do hidrogênio no centro da folha para o dobro do valor-limite calculado na parte (a), ou seja:
Substituindo no parâmetro:
Nós temos que tudo, não é? Então vamos substituir:
E chegamos ao fim de mais umaa !!