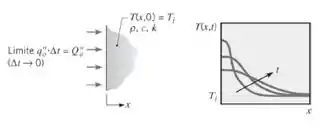
Se uma quantidade de energia for liberada instantaneamente, por exemplo, a partir de um laser pulsante, e ela for absorvida pela superfície de um meio semi-infinito, sem perdas concomitantes para o ambiente, a distribuição de temperaturas subsequente no meio é

sendo Ti a temperatura inicial e uniforme do meio. Considere um processo de transferência de massa análogo envolvendo a deposição de uma fina camada de fósforo (P) sobre uma pastilha de silício (Si) à temperatura ambiente. Se a pastilha estiver colocada em um forno, a difusão do P no Si é aumentada significativamente pelo ambiente a alta temperatura.

Uma pastilha de Si com um filme de P com espessura de 1 μm é subitamente colocada em um forno a 1000°C e a distribuição resultante de P é caracterizada por uma expressão com a forma:

sendo a concentração superficial molar de P associada ao filme de concentração e espessura .

1. Explique a correspondência entre variáveis nas distribuições de temperaturas e de concentrações análogas.
2. Determine a fração molar de P a uma profundidade de 0,1 μm no Si após 30 s. O coeficiente de difusão é . As concentrações mássicas do P e do Si são 2000 e 2300 kg/m³, respectivamente, e suas massas molares são 30,97 e 28,09 kg/kmol.

Bom galerinha, na letra (b) queremos a fração molar de P na placa, sabendo que:

Nós já sabemos que:

A única coisa que não temos é , mas para calcular vamos usar uma fórmula muito simples:

A concentração pode ser escrita como:

Substituindo:

E na fórmula do problema:

Achamos uma informação importante, mas ainda não é o que procuramos!

O que queremos é a fração molar, ou seja:

Então ainda precisamos de achar

Mas usando uma fórmula similar ao que vimos no comecinho deste Passo:

Substituindo na fórmula do que queremos:

E colocando os dados:

Sendo assim, quando estamos a uma distância de e 30 s a fração de fósforo é

Shoooow !! Acabamos mais umaa !!