Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Brunetti - Mecânica dos Fluidos - Ed: 2º - Capítulo 5.Exercício - Ex. 6

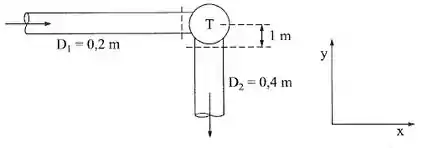
Na instalação esquematizada na figura, (T) é uma turbina e o fluido que escoa é água de massa específica ρ = 1000   k g / m 3 . A vazão que escoa é 314 L/s e as pressões em (1) e (2) são, respectivamente, p 1 = 18   N / c m 2 e p 2 = - 2   N / c m 2 . Desprezam-se as perdas. Determinar:

a) a potência consumida pela turbina;

b) o esforço segundo x que atua na base da turbina.

Adotar g = 10   m / s 2 e A 1 = 0,0314   m 2   ( D 1 = 0,20   m ) .

Passo 1

Vamos começar encontrando as velocidades nos pontos 1 e 2 através da vazão:

Q = v 1 A 1 → v 1 = Q A 1 = 314.10 - 3 0,0314 → v 1 = 10   m / s

Q = v 2 A 2 → v 2 = Q A 2 = Q π D 2 2 4 = 314.10 - 3 π 0,4 2 4 → v 2 = 2,5   m / s

Passo 2

Agora vamos aplicar a equação para o equilíbrio de cargas entre os pontos 1 e 2:

H 1 - H T = H 2

v 1 2 2 g + p 1 γ + z 1 - H T = v 2 2 2 g + p 2 γ + z 2

Substituindo os valores conhecidos, temos:

10 2 2 10 + 18.10 4 10 4 + 1 - H T = 2,5 2 2 10 + - 2.10 4 10 4 + 0 → H T = 25,7   m

A equação que representa a potência da turbina é dada por:

N = γ Q H T = 10 4 314.10 - 3 25,7 → N = 80698   W

Passo 3

Antes de aplicarmos a equação da força, vamos encontrar a vazão mássica do sistema, que é dada por:

Q m = ρ Q = 1000 0,314 → Q m = 314   k g / s

A equação que representa a força que o fluido exerce é dada por:

F → s = - p 1 A 1 n → 1 + p 2 A 2 n → 2 + Q m v → 2 - v → 1

Agora vamos calcular a componente em x ( → ) :

F s x = - p 1 A 1 - 1 + p 2 A 2 0 + Q m 0 - v 1

Substituindo os valores conhecidos:

F s x = - 18.10 4 ( 0,0314 ) - 1 + 0 + 314 - 10

F s x = 8792   N

Resposta

N = 80698   W

F s x = 8792   N

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Sabendo que o sistema da figura encontra-se em equilíbrio, desprezando as perdas, determinar a altura h 0 . ( γ H 2 O = 10 4N / m 3 ; γ = 2.10 4N / m 3 ; A p = 8.10 - 3m 2 ; h 1 = 78,5c m ; Q = 15,7L
No tanque da figura, determinar a força F s x que deve ser aplicada para que ele permaneça parado. Qual é o diâmetro do bocal que deverá ser instalado na parede oposta ao bocal mostrado na figura, par
Considerando que na região de escoamento completamente desenvolvido de um tubo, a integral da quantidade de movimento axial é a mesma em todas as seções transversais, explique a razão para a queda de
Para as condições do Problema 4.34, avalie a razão entre o fluxo de quantidade de movimento na direção x na saída do canal e aquele na entrada.
Para as condições do Problema 4.35, avalie a razão entre o fluxo de quantidade de movimento na direção x na saída do canal e aquele na entrada.