Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Brunetti - Mecânica dos Fluidos - Ed: 2º - Capítulo 5.Exercício - Ex. 2
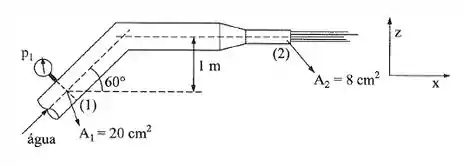
Sabendo que a perda de carga no trecho (1)-(2) é 3 m, determinar as componentes horizontal e vertical da força aplicada pelo fluido nesse trecho de tubulação. Dados: ; .
Passo 1
Vamos começar o exercício calculando as velocidades nos pontos 1 e 2 através da vazão:
Agora vamos aplicar o equilíbrio de cargas entre os pontos 1 e 2:
Substituindo os valores conhecidos, podemos encontrar o valor de :
Passo 2
A equação que representa a força que o fluido exerce é dada por:
Agora vamos calcular primeiro a componente em :
Sabemos que , então a equação se torna:
Substituindo os valores conhecidos, temos:
Passo 3
Agora vamos calcular a componente em :
Então a equação se torna:
Substituindo os valores conhecidos, temos:
Resposta
Exercícios de Livros Relacionados
Avalie o fluxo líquido de quantidade de movimento através do canal do Problema 4.38, se a profundidade normal ao diagrama for w = 1m .
Avalie o fluxo líquido de quantidade de movimento através do canal do Problema 4.39. Você esperaria que a pressão na saída fosse maior, menor ou a mesma que a pressão na entrada? Por quê?
Em um experimento laboratorial, a vazão de água deve ser medida capturando-a conforme a água sai verticalmente de um tubo dentro de um tanque aberto e vazio que está sobre uma balança zerada. O fundo
Obtenha expressões para a taxa de variação em massa do volume de controle mostrado, bem, como as forças horizontal e vertical requeridas para manter o volume de controle fixo, em função de P 1 ,A 1 ,V
Calcule a força requerida para manter o tampão fixo na saído do tubo de água. A vazão é 1,5m 3 / s e a pressão a montante é 3,5M P a .