Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Brunetti - Mecânica dos Fluidos - Ed: 2º - Capítulo 5.Exercício - Ex. 8

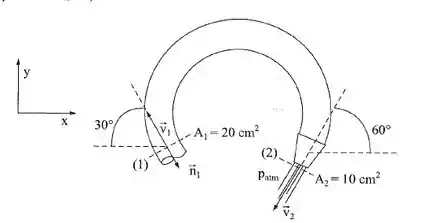
No trecho (1)-(2) da tubulação, que está num plano horizontal, escoa água em regime permanente. A perda de carga de (1) a (2) é 10 m e a vazão, 10 L/s. Qual é a força resultante aplicada pelo fluido na tubulação? ( γ = 10000   N / m 3 )

Passo 1

Vamos começar o exercício calculando a velocidade nos pontos 1 e 2 através da vazão fornecida:

Q = v 1 A 1 → v 1 = Q A 1 = 10.10 - 3 20.10 - 4 → v 1 = 5   m / s

Q = v 2 A 2 → v 2 = Q A 2 = 10.10 - 3 10.10 - 4 → v 2 = 10   m / s

E vamos encontrar também a vazão mássica do sistema, dada por:

Q m = ρ Q = 1000 10.10 - 3 → Q m = 10   k g / s

Agora vamos aplicar o equilíbrio de carga entre os pontos 1 e 2 para descobrir o valor da pressão na entrada:

H 1 = H 2 + H p 1,2

v 1 2 2 g + p 1 γ + z 1 = v 2 2 2 g + p 2 γ + z 2 + H p 1,2

Substituindo os valores conhecidos, temos:

5 2 2 10 + p 1 10 4 + 0 = 10 2 2 10 + 0 10 4 + 0 + 10 → p 1 = 137,5   k P a

Passo 2

Agora vamos aplicar a equação para a força exercida pelo fluido, dada por:

F → s = - p 1 A 1 n → 1 + p 2 A 2 n → 2 + Q m v → 2 - v → 1

Vamos aplicar a equação na direção x ( → ) :

F s x = - p 1 A 1 cos ⁡ 30 ° + ( 0 ) A 2 - cos ⁡ 60 ° + Q m - v 2 cos ⁡ 60 ° + v 1 cos ⁡ 30 °

Substituindo os valores conhecidos, temos:

F s x = - 137,5.10 3 20.10 - 4 3 2 + 0 + 10 - 10 1 2 + 5 3 2

F s x = - 231,5   N

Passo 3

Agora iremos aplicar novamente a equação da força, dada por:

F → s = - p 1 A 1 n → 1 + p 2 A 2 n → 2 + Q m v → 2 - v → 1

Agora vamos calcular a componente em y ( ↑ ) :

F s y = - p 1 A 1 - sen ⁡ 30 ° + ( 0 ) A 2 - sen ⁡ 60 ° + Q m - v 2 sen ⁡ 60 ° - v 1 sen ⁡ 30 °

Substituindo os valores conhecidos:

F s y = - 137,5.10 3 20.10 - 4 1 2 + 0 + 10 - 10 3 2 - 5 1 2

F s y = 249,1   N

Agora podemos encontrar a intensidade da força resultante através de:

F s = F s x 2 + F s y 2 = - 231,5 2 + 249,1 2 → F s = 340,1   N

Resposta

F s = 340,1   N

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um propulsor a jato queima 1 kg/s de combustível. Calcular a força de propulsão, quando o avião voa à velocidade constante de 200 m/s. Dados: ρ a r = 1,2k g / m 3 ; ρ g a s e s = 0,5k g / m 3 ; A 1 =
Dados D 1 = 10c m ; ρ = 1000k g / m 3 ; H p 0,1 = 2,8m ; D 2 = 8c m ; H p 0 , e = 1,5m ; H p s , 2 = 2,4m ; η B = 0,7 . Calcular:a) a potência no eixo da bomba para que o corpo apoiado nas rodas sem a
Um jato atinge uma pá que se localiza num plano inclinado. O peso do conjunto é 40 N e a área do jato é 50 cm². Qual deverá ser a velocidade do jato para que o sistema permaneça em equilíbrio? ( γ = 1
Dado o esquema da figura, sabendo que a seção do jato tem uma área de 520 cm² e que a área do pistão é 20 cm², determinar a vazão no bocal. Dados: γ H 2 O = 10 4N / m 3 ; γ H g = 1,36.10 5N / m 3 . Ob
Um fabricante de brinquedos constrói um carrinho impulsionado pelo ar de uma bexiga. No instante inicial em que é liberado o ar, determinar:a) a força de propulsão;b) a pressão do ar da bexiga, despre