Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Brunetti - Mecânica dos Fluidos - Ed: 2º - Capítulo 7.Exercício - Ex. 12
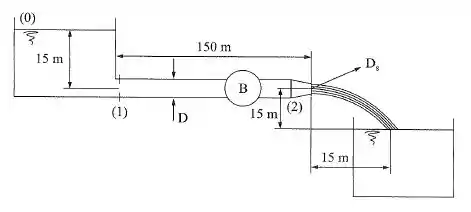
Na instalação da figura, a água deve ser lançada por meio de um bocal no tanque da direita. Determinar a mínima potência da bomba para que isso aconteça. Dados: material: ferro fundido; diâmetro de saída ; ; ; . Desprezar a perda singular no bocal.
Passo 1
Antes de começar o exercício, devemos lembrar um pouquinho do movimento parabólico em queda livre e sem velocidade inicial na direção , dessa forma, as equações para o deslocamento em e são:
Substituindo a primeira relação na segunda, obtemos:
Então, substituindo as medidas de distância da figura do enunciado, temos:
Essa velocidade que encontramos é a velocidade de saída do bocal , agora, para encontrar a velocidade do escoamento dentro da tubulação, vamos usar a igualdade entre as vazões nesses dois pontos, então, temos:
Substituindo os valores conhecidos:
Passo 2
Agora vamos aplicar o equilíbrio de energia ao sistema entre os pontos 0 e o ponto de saída do bocal :
Como nesse casos temos perda distribuída e localizada, a equação se torna:
Passo 3
Nós sabemos que a perda de carga distribuída é dada por:
Como não temos o valor de , devemos recorrer ao diagrama de Moody a seguir, para isso precisamos encontrar o valor de , nesse caso, como temos uma seção circular, então e a equação se torna (note que o valor de para o ferro fundido se encontra no quadro dentro do diagrama de Moody):
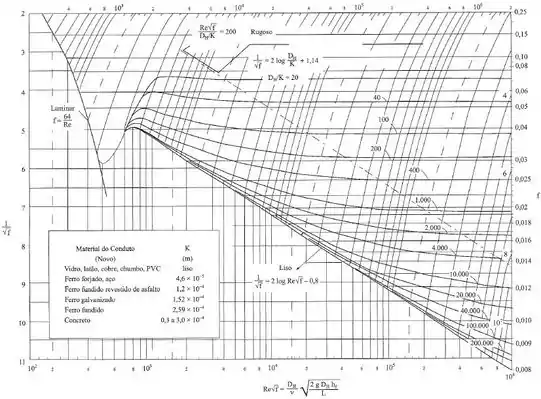
Agora vamos encontrar o valor de Reynolds para descobrir em que faixa de escoamento o exercício se encontra:
Para esse valor de Reynolds, o escoamento é rugoso, que é a parcela onde as curvas possuem um valor constante (ocorrem para altos valores de ), dessa forma, para a relação encontrada, vamos adotar:
Agora podemos retornar a equação da perda de carga distribuída:
Passo 4
Agora vamos retornar à equação de equilíbrio de energia do passo 2:
Substituindo os valores conhecidos, temos:
E, antes de calcular a potência da bomba, precisamos encontrar a vazão do sistema, faremos isso usando a velocidade dentro da tubulação antes do bocal encontrada lá no passo 1:
Agora podemos aplicar a equação da potência para a bomba, dada por: