Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Brunetti - Mecânica dos Fluidos - Ed: 2º - Capítulo 7.Exercício - Ex. 24

O escoamento no trecho do tubo da figura é laminar. Com a válvula totalmente aberta, a linha piezométrica é praticamente uma reta e indica as medidas do desenho. Ao fechar a válvula de 3/4, a vazão cai à metade da anterior. Determinar o coeficiente de perda de carga singular nesse caso, sabendo que na segunda situação o desnível marcado pelos manômetros extremos é o mesmo da primeira situação.

Dados: ; ; .

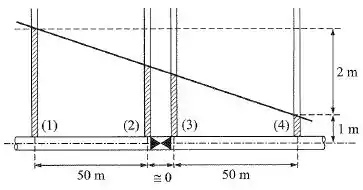
Passo 1

Conforme sabemos, quando temos a linha de energia formando um certo ângulo com a horizontal e não temos perdas localizadas nesse trecho, então podemos escrever a perda de carga distribuída em função desse ângulo:

Abrindo a expressão, temos:

Passo 2

No entanto, o enunciado nos disse que o escoamento é laminar, e através da equação 7.11, apresentada nessa seção, podemos encontrar :

Substituindo essa expressão na última equação do passo 2, temos:

Isolando da expressão e substituindo os valores conhecidos, temos:

Como o enunciado nos disse que a vazão cai a metade quando a válvula se fecha de 3/4, como a geometria do tubo se mantém constante, então a velocidade também cai à metade, de forma que temos:

Então, conforme indicado pela linha de energia no esquema do enunciado, a perda de carga total equivale a 2 m, dessa forma, temos:

Para o segundo caso, abrindo a expressão e substituindo os valores conhecidos, temos:

Passo 3

Agora podemos usar a equação para a perda de carga singular para encontrar o coeficiente de perda de carga singular, então, temos:

Substituindo os valores conhecidos:

Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Querosene é bombeado através de um tubo liso com diâmetro interno D = 30 mm, na proximidade do número de Reynolds crítico. O escoamento é instável e flutua entre os estados laminar e turbulento, fazen

Foi sugerido, no projeto de um “sprinkler” agrícola, que um elemento estrutural fosse mantido fixo por meio de um arame esticado ao longo da linha de centro de um tubo; acreditava-se que um arame rela

A seguinte solução: u = u 0 1 - y 2 a 2 - z 2 b 2 pode ser usada como um modelo para o perfil de velocidade de um escoamento pressurizado completamente desenvolvido em um canal com seção transversal e

Um medicamento líquido, com a viscosidade e a massa específica da água, deve ser administrado através de uma agulha hipodérmica. O diâmetro interno da agulha é 0,25 mm e o seu comprimento é de 50 mm.

O clássico escoamento de Poiseuille (Eq. 8.12) mostra a condição de não deslizamento na parede. Se o fluido é um gás, e quando o livre caminho médio l (distância média que uma molécula viaja antes de