Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Brunetti - Mecânica dos Fluidos - Ed: 2º - Capítulo 2.Exercício - Ex. 23

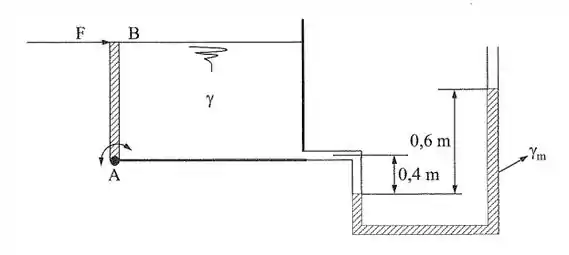
Na instalação da figura, a comporta quadrada A B , que pode girar em torno de A, está em equilíbrio devido à ação da força horizontal F . Sabendo que γ m = 80.000   N / m 3 e γ = 30.000   N / m 3 , determinar o valor da força F .

Passo 1

Oi pessoal, tudo bem? Vamos analisar essa questão.

O exercício nos pede a força F que sustenta a comporta. Vamos chamar de L a altura da comporta. Temos a seguinte situação:

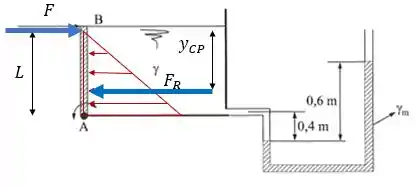
Podemos encontrar o valor de L aplicando a equação manométrica, temos que:

P a t m + L γ + 0,4 γ - 0,6 γ m = P a t m

L = 0,6 γ m - 0,4 γ γ

L = 0,6 80000 - 0,4 ( 30000 ) 30000

L = 1,2   m

Passo 2

Ainda observando nosso diagrama do passo anterior, podemos dizer que F R que é a força resultante causada pelo fluido deve causar um momento em A igual ao momento que F causa em A . Logo:

F ⋅ L = F R ⋅ L - y C P

Para descobrirmos o centro de pressão da força resultante temos a seguinte equação:

y C P = y C G + I C G y C G A

Onde:

y C G = L 2

I C G = L ⋅ L 3 12 = L 4 12

A = L 2

Substituindo, temos que:

y C P = L 2 + L 4 12 L 2 L 2

Resolvendo, temos que:

y C P = L 2 + L 6 = 2 3 L

y C P = 0,8   m

Passo 3

A força resultante é dada pela multiplicação da pressão no centro de gravidade pela área. Ou seja:

F R = γ y C G ⋅ A

F R = 30000 1,2 2 1,2 2

F R = 25920   N

Portanto:

F ⋅ L = F R ⋅ L - y C P

F ⋅ 1,2 = 25920 ⋅ 1,2 - 0,8

F = 8640   N

Resposta

F = 8640   N

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determinar a força, devido à pressão da água, na comporta retangular da figura, sendo o peso específico do fluido 10.000N / m 3 .
Determinar o módulo e o ponto de aplicação das componentes horizontal e vertical da força exercida pela água sobre a comporta A B da figura, sabendo que sua largura é 0,3m , o raio é 1,8m e a comporta
A comporta A B da figura tem 1,5m de largura e pode girar em torno de A . O tanque à esquerda contém água ( γ = 10.000N / m 3 ) e o da direita, óleo ( γ = 7.500N / m 3 ) . Qual é a força necessária em
Sabendo que γ 1 = 6 γ 2 , calcular a relação x / h para que a comporta permaneça em equilíbrio na posição indicada na figura. Desprezar o peso próprio da comporta.
No esquema da figura, determinar a altura h e a mínima força F para que a comporta A B C permaneça em equilíbrio. Dados: largura = 1,5m ; γ H g = 136000N / m 3 ; γ H 2 O = 10000N / m 3 .