Sabendo que , calcular a relação para que a comporta permaneça em equilíbrio na posição indicada na figura. Desprezar o peso próprio da comporta.
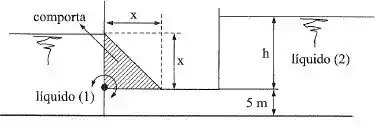
Passo 1
Oi pessoal, tudo bem? Vamos analisar essa questão.
Temos os seguintes prismas de pressão gerado na comporta, com seus valores máximos descritos na imagem abaixo:
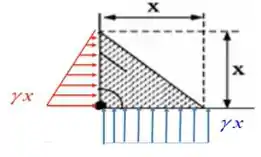
A força gerada pelo triângulo chamaremos de e como trata-se de um triângulo, sabemos que o seu centro de aplicação é do ponto superior, logo:
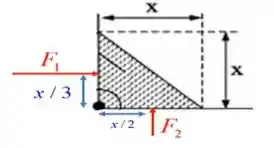
Passo 2
A condição de equilíbrio é de que o momento gerado pela força seja igual ao momento gerado pela força , portanto:
Logo:
Como as áreas são iguais, temos que:
Passo 3
Como estamos trabalhando com as pressões no centro de gravidade, temos que:
A altura do centro de gravidade da parte é e a altura do centro de gravidade da parte é , portanto:
Como nos foi dito que , temos que:
Logo: