Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 8.Problemas - Ex. 102

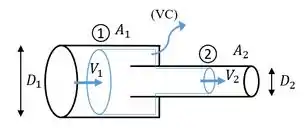
Água escoa de um grande tubo, de diâmetro, de D 1 = 100   m m , e entra em um tubo menor, de diâmetro D 2 = 500   m m , por meio de um dispositivo reentrante. Encontre a perda de carga entre os pontos 1 e 2 . Considere Q = 0,01   m 3 / s .

Passo 1

Neste problema é pedido a a perda de carga entre os pontos 1 e 2.

Será utilizada a Equação da energia na forma:

p 1 ρ 1 + α V 1 2 2 + g z 1 = p 2 ρ 2 + α V 2 2 2 + g z 2 + h l T

Sendo a perda de carga total definida como:

h l T = f L D V 2 2   2   + K V 2 2 2

Como hipótese e dados do enunciado tem-se que;

- regime permanente ( ∂ / ∂ t = 0 );

- escoamento horizontal ( z 1 = z 2 );

- escoamento incompressível ( ρ 1 = ρ 2   e ρ á g u a = 1000   k g / m 3 );

- α ≈ 1,0 ;

- D 1 = 100   m m ;

- D 2 = 50   m m ;

- L ≈ 0 (tubo de pequeno comprimento);

- Q = 0,01   m 3 / s .

Passo 2

Usando a Equação de Energia, em J/kg, entre as seções 1 e 2:

p 1 ρ 1 + α V 1 2 2 + g z 1 = p 2 ρ 2 + α V 2 2 2 + g z 2 + h l T

p 1 ρ - p 2 ρ = α V 2 2 2 - α V 1 2 2 + g z 2 - g z 1 + h l T

p 1 - p 2 = + ρ α V 2 2 - V 1 2 2 + ρ g z 2 - z 1 + ρ h l m

Sabendo a expressão de h l m , que z 1 = z 2 e α ≈ 1 :

p 1 - p 2 = ρ V 2 2 - V 1 2 2 + ρ f L D V 2 2   2   + ρ K V 2 2 2

Mas pela hipótese de comprimento do tubo curto:

ρ f L D V 2 2   2 ≈ 0

Então a queda de pressão é dada por:

p 1 - p 2 = ρ V 2 2 - V 1 2 2   + ρ K V 2 2 2

Passo 3

Uma informação importante de escoamento com perda de carga em tubulação horizontal é que a queda de pressão é igual a perda de carga, ou seja:

p 1 - p 2 ρ = h

Então reescrendo a expressão de p 1 - p 2 do Passo 2:

ρ h = ρ V 2 2 - V 1 2 2   + ρ K V 2 2 2

Logo, a perda de carga pode ser escrita como:

h = V 2 2 - V 1 2 2   + K V 2 2 2

Passo 4

Escrevendo as velocidade em termo dos parâmetros dados no enunciado:

Q = V 1 A 1 = V 2 A 2

Logo:

V 1 = Q A 1

V 1 = Q A 2

Passo 5

Então a expressão da perda de carga poderá ser escrita como;

h = Q A 2 2 - Q A 1 2 2   + K Q A 2 2 2

h = Q A 2 2 2   1 - A 2 A 1 2 + K

Passo 6

Sabendo que a relação de áreas A 2 / A 1 é dada por:

A 2 A 1 = π D 2 2 4 π D 1 2 4 = D 2 2 D 1 2

A 2 A 1 = 50 × 10 - 3 2 100 × 10 - 3 2 = 0,25

Já as áreas têm os seguintes valores:

A 1 = π D 1 2 4 = π × 100 × 10 - 3 2 4 = 7,85 × 10 - 3   m 2

A 2 = π D 2 2 4 = π × 50 × 10 - 3 2 4 = 1,96 × 10 - 3   m 2

Então pela Tabela 8.2, considerando tubo reentrante, o coeficiente de perda de carga para a expansão vale:

K = 0,78

Passo 7

Então, a perda de carga será:

h = Q A 2 2 2   1 - A 2 A 1 2 + K

h = 0,01 1,96 × 10 - 3 2 2   1 - 0,25 2 + 0,78

h = 22,35   J / k g

Já a perda de carga em m é dada por:

H = h g

H = 22,35 9,81

Logo, a perda de carga em metros vale:

H ≅ 2,28   m

Resposta

H ≅ 2,28   m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O professor Gordon Holloway e seus alunos na Universidade de New Brunswick foram a uma lanchonete e tentaram tomar milkshakes de chocolate ( ρ = 1200k g / m ³ , ³ μ = 6k g / ( m . s ) por meio de canu
Um tubo capilar de 5 mm de diâmetro é usado como um viscosímetro para óleos. Quando a vazão é de 0,071 m³/h, a queda de pressão por unidade de comprimento medida é 375 kPa/m. Calcule a viscosidade do
Para a configuração mostrada abaixo, o fluido é álcool etílico a 20°C, e os reservatórios são muito grandes. Determine a vazão que ocorre em m³/h. O escoamento é laminar?
Uma compressão constante sobre o pistão da figura abaixo produz uma vazão Q = 0,15c m 3 / s através da agulha. O fluido tem ρ = 900k g / m ³ ³ e μ = 0,002k g / ( m . s ) . Qual a força F necessária pa
Água a 20°C deve ser retirada por sifão por um tubo de 1 m de comprimento e 2 mm de diâmetro, como na figura a seguir. Existe alguma altura H para a qual o escoamento não é laminar? Qual é a vazão se