Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Brunetti - Mecânica dos Fluidos - Ed: 2º - Capítulo 7.Exercício - Ex. 27

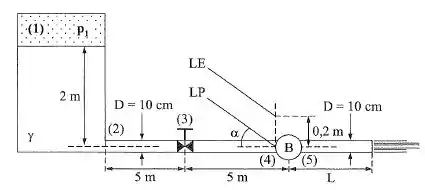
Na instalação da figura, a potência da bomba é 1,57 kW. Determinar a pressão p 1 e o comprimento L, sabendo que k s 2 = 1 ; k s 3 = 0,5 ; tg ⁡ α = 0,004 ; η B = 80 % e γ = 10 4   N / m 3 . Deseja-se substituir as perdas singulares por perdas distribuídas (para facilitar os cálculos). Qual deverá ser o comprimento da tubulação a ser acrescentado nos cálculos?

Passo 1

Como temos o valor da tg ⁡ α e sabemos que a diferença de altura nesse trecho corresponde a perda de carga distribuída, podemos escrever:

tg ⁡ α = h f 1,4 L 1,4

Substituindo os valores conhecidos:

0,004 = h f 1,4 10 → h f 1,4 = 0,04   m

Vamos agora encontrar a velocidade do escoamento, faremos isso usando a diferença de altura entre as linhas LE e LP, que representam a carga cinética, que é dada por:

L E - L P = 0,2 = v 2 2 g → v 2 = 0,2 2 10 → v = 2   m / s

Agora vamos usar a velocidade para encontrar o valor da vazão no sistema:

Q = v A = v π D 2 4 = 2 π 0,1 2 4 → Q = 1,57.10 - 2   m 3 / s

Passo 2

Agora vamos encontrar o valor das perdas de carga localizadas nos pontos 2 e 3:

h s 2 = k s 2 v 2 2 g = 1 2 2 2 10 → h s 2 = 0,2   m

h s 3 = k s 3 v 2 2 g = 0,5 2 2 2 10 → h s 3 = 0,1   m

Agora, sabemos que a perda total entre os trechos 1 e 4 será:

H p 1,4 = h s 2 + h s 3 + h f 1,4 = 0,2 + 0,1 + 0,04 → H p 1,4 = 0,34   m

Com esse valor, podemos aplicar o equilíbrio de energia entre os pontos 1 e 4:

H 1 = H 4 + H p 1,4

v 1 2 2 g + p 1 γ + z 1 = v 4 2 2 g + p 4 γ + z 4 + H p 1,4

Substituindo os valores conhecidos, temos:

0 2 2 g + p 1 10 4 + 2 = 2 2 2 10 + 0 + 0 + 0,34 → p 1 = - 14600   P a

Passo 3

Agora, para substituir as perdas singulares por perdas distribuídas, precisamos primeiro descobrir o valor da perda de carga entre os pontos 4 e 6 (saída da tubulação). Só que para isso, precisamos antes encontrar o valor da carga da bomba, que pode ser encontrado através da equação para sua potência, que é dada por:

N B = γ Q H B η B → H B = N B η B γ Q

Substituindo os valores conhecidos:

H B = 1,57.10 3 0,8 10 4 1,57.10 - 2 → H B = 8   m

Agora vamos aplicar o equilíbrio de energia entre os pontos 4 e 6:

H 4 + H B = H 6 + H p 5,6

v 4 2 2 g + p 4 γ + z 4 + H B = v 6 2 2 g + p 6 γ + z 6 + H p 5,6

Substituindo os valores conhecidos:

2 2 2 10 + 0 γ + 0 + 8 = 2 2 2 10 + 0 γ + z 6 + H p 5,6 → H p 5,6 = 8   m

Passo 4

Agora, para encontrar o comprimento L desse trecho, podemos voltar à primeira equação do passo 1 e aplica-la para esse trecho, sabendo que só temos perda distribuída, então, temos:

tg ⁡ α = h f 5,6 L 5,6 → 0,004 = 8 L 5,6 → L = 2000   m

Passo 5

Agora, para substituírmos as perdas singulares pelo comprimento equivalente, podemos igualar as perdas singulares encontradas no passo 2 à nova perda equivalente, então temos:

h s 2 + h s 3 = h f e q

E, usando novamente a relação trigonométrica, temos:

tg ⁡ α = h f e q L e q → h f e q = L e q tg ⁡ α

Substituindo essa expressão na equação anterior:

h s 2 + h s 3 = L e q tg ⁡ α

Substituindo os valores conhecidos, temos:

0,2 + 0,1 = L e q 0,004 → L e q = 75   m

Resposta

p 1 = - 14600   P a

L = 2000   m

L e q = 75   m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Numa fábrica constrói-se um trocador de calor, cujos diâmetros de entrada e saída são 10c m . Para determinar o comprimento equivalente do trocador, constrói-se o circuito da figura, no qual todas as
Uma grande massa é suportada por um pistão de diâmetro D = 100m m e comprimento L = 100m m . O pistão está assentado em um cilindro fechado no fundo. A folga a = 0,025m m entre a parede do cilindro e
Uma alta pressão em um sistema é criada por um pequeno conjunto pistão-cilindro. O diâmetro do pistão é 6 mm e ele penetra 50 mm no cilindro. A folga radial entre o pistão e o cilindro é 0,002 mm. Des
Um macaco hidráulico suporta uma carga de 9000 kg. Os seguintes dados estão disponíveis:Diâmetro do pistão: 100 mmFolga radial entre o pistão e o cilindro: 0,05 mmComprimento do pistão: 120 mmEstime a
Um óleo viscoso escoa em regime permanente entre duas placas paralelas estacionárias. O escoamento é laminar e completamente desenvolvido. O espaçamento entre as placas é h = 5m m . A viscosidade do ó