Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Brunetti - Mecânica dos Fluidos - Ed: 2º - Capítulo 7.Exercício - Ex. 19
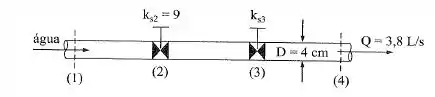
Na figura, e os comprimentos equivalentes das singularidades são e . Determinar:
a) o coeficiente de perda de carga distribuída ;
b) o comprimento da instalação entre (1) e (4);
c) a perda de carga singular devida à válvula (3).
Passo 1
Tá legal! Para resolver a letra a), basta que lembremos como é a fórmula da perda de carga distribuída e localizada, pois temos o comprimento equivalente da perda da singularidade e podemos igualar as duas perdas para obter o fator , então, a perda distribuída é:
E a perda localizada:
Então, aplicando as equações para a singularidade 2, temos:
Igualando as duas equações, temos:
Simplificando a expressão e isolando , temos:
Passo 2
Agora para achar o comprimento total da instalação, podemos encontrar o comprimento equivalente total e depois subtrair as duas parcelas equivalentes da singularidade dadas no enunciado. Então vamos começar escrevendo a fórmula da perda de carga entre os pontos 1 e 4 para o comprimento equivalente total:
Agora, aplicando o equilíbrio de energia entre os pontos 1 e 4 podemos encontrar o valor da perda de carga total do sistema:
Como não temos mudança de geometria da tubulação, as velocidades nos pontos 1 e 4 são iguais, então, substituindo os valores conhecidos, temos:
Agora precisamos encontrar o valor da velocidade do escoamento, faremos isso usando a fórmula da vazão:
Substituindo esse valor e os outros conhecidos na primeira equação do passo 2, temos:
Agora, o comprimento real entre 1 e 4 será:
Passo 3
Agora para a letra c), podemos novamente igualar as perdas de carga distribuída e localizada como fizemos no passo 1, só que para o ponto 3, então, temos:
Substituindo os valores conhecidos, temos: