Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Brunetti - Mecânica dos Fluidos - Ed: 2º - Capítulo 7.Exercício - Ex. 9
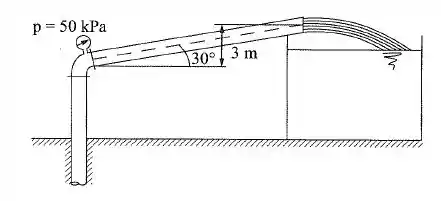
Um pequeno reservatório é alimentado por um poço artesiano, conforme mostra a figura. O manômetro metálico acusa 50 kPa. Sabe-se que a tubulação é de ferro fundido de 10 cm de diâmetro. Calcular a vazão de alimentação do reservatório.
Passo 1
Vamos começar o exercício aplicando o equilíbrio de energia entre os pontos 1 (ponto onde está instalado o manômetro aferindo 50 kPa) e 2 (saída da tubulação):
Substituindo os termos conhecidos:
Nesse caso, como sabemos que a vazão deve ser constante e o diâmetro da tubulação não se altera, então , logo, podemos cancelar os termos da velocidade que aparecem dos dois lados da equação, então, isolando temos:
Passo 2
Sabemos que a perda de carga distribuída é dada por:
Isolando da equação, temos:
Como não temos o valor de , devemos recorrer ao diagrama de Moody a seguir, para isso precisamos encontrar o valor de , nesse caso, como temos uma seção circular, então , nesse caso, temos (lembrando que no próprio diagrama temos o valor de para o ferro fundido, material de que é feito o tubo do exercício):
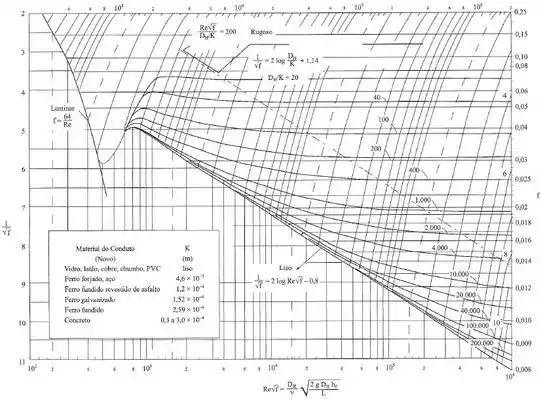
Lembrando que sempre supomos um valor na parte do diagrama onde o escoamento é rugoso, que é a parcela onde as curvas possuem um valor constante (ocorrem para altos valores de ), dessa forma, para a relação encontrada, vamos adotar:
Agora podemos retornar a equação da velocidade obtida e substituir os valores conhecidos:
Agora precisamos verificar se o valor que assumimos para foi coerente, para isso, vamos calcular Reynolds
Então, para esse valor de Reynolds, podemos ver no diagrama de Moody que a já se encontra constante, então nossa suposição foi válida.
Passo 3
Então agora podemos calcular o valor da vazão para o sistema: