Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Brunetti - Mecânica dos Fluidos - Ed: 2º - Capítulo 4.Exercício - Ex. 30

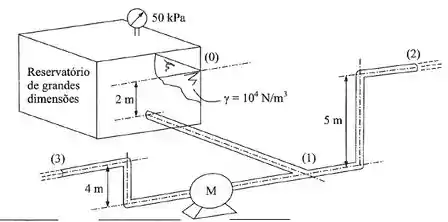
Na instalação da figura, todas as tubulações são de diâmetro muito grande em face da vazão, o que torna desprezível a carga cinética. Determinar:

a) o tipo de máquina e a sua carga manométrica;

b) a vazão em volume proveniente do reservatório;

Dados: Q 2 = Q 3 ; H p 0,1 = 1   m ; H p 1,2 = 1   m ; H p 1,3 = 4   m ; η m = 80 % ; potência no eixo da máquina = 0,7 kW

Passo 1

Vamos começar o exercício calculando a carga no ponto 0:

H 0 = v 0 2 2 g + p 0 γ + z 0 = 0 + 50.10 3 10 4 + 2 → H 0 = 7   m

Da mesma forma, calculando as cargas nos pontos 2 e 3, conforme foi dito para desprezar a parcela cinética, temos:

H 2 = v 2 2 2 g + p 2 γ + z 2 = 0 + 0 10 4 + 5 → H 2 = 5   m

H 3 = v 3 2 2 g + p 3 γ + z 3 = 0 + 0 10 4 + 4 → H 3 = 4   m

Lembrando que o enunciado nos disse que Q 2 = Q 3 , então, através disso e do desenho da instalação, podemos escrever a vazão Q 0 em termo de uma das duas vazões:

Q 0 = Q 2 + Q 3 = Q 2 + Q 2 → Q 0 = 2 Q 2 → Q 2 = Q 0 2

E, como Q 2 e Q 3 são iguais:

Q 3 = Q 0 2

Passo 2

Agora vamos usar o princípio da conservação da energia para o sistema, assim, temos:

γ Q 0 H 0 + γ Q 3 H M = γ Q 2 H 2 + γ Q 3 H 3 + γ Q 0 H p 0,1 + γ Q 2 H p 1,2 + γ Q 3 H p 1,3

Agora vamos substituir os valores conhecidos na equação:

10 4 Q 0 ( 7 ) + 10 4 Q 0 2 H M = 10 4 Q 0 2 ( 5 ) + 10 4 Q 0 2 ( 4 ) + 10 4 Q 0 ( 1 ) + 10 4 Q 0 2 ( 1 ) + 10 4 Q 0 2 ( 4 )

Simplificando a expressão (notando que os termos Q 0 e 10 4 aparecem em todos os termos) temos:

7 + H M 2 = 2,5 + 2 + 1 + 0,5 + 2 → H M = 2   m

Como a carga obtida é positiva, sabemos que a máquina fornece energia ao fluido, logo, a máquina deve ser uma bomba.

Passo 3

Agora vamos calcular a vazão no ponto 3 (após a bomba) através da equação de sua potência, dada por:

N B = γ Q 3 H B η B → Q 3 = N B η B γ H B = 700 0,8 10 4 2 → Q 3 = 0,028   m 3 / s

E, substituindo esse valor na expressão para Q 0 (vazão do reservatório) obtida no passo 1:

Q 0 = 2 Q 3 = 2 0,028 → Q 0 = 0,056   m 3 / s

Resposta

H M = 2   m   ( b o m b a )

Q 0 = 0,056   m 3 / s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um tubo de Pitot é preso num barco que se desloca com 45k m / h . Qual será a altura h alcançada pela água no ramo vertical.
Dado o dispositivo da figura, calcular a vazão do escoamento da água do conduto.Dados: γ H 2 O = 10 4N / m 3 ; γ m = 6 × 10 4N / m 3 ; p 2 = 20k P a ; A = 10 - 2m ² ² g = 10m / s 2 . Desprezar as perd
Dados: H p 2,3 = 2m ; A 3 = 20c m 2 ; A 2 = 1c m 2 ; H p 0,1 = 0,8m ; η B = 70 % . Determinar:a vazão ( L / s ) ;a área da seção 1 c m 2 ;a potência fornecida pela bomba ao fluido.
Num carburador, a velocidade do ar na garganta do Venturi é 120m / s . O diâmetro da garganta é 25m m . O tubo principal de admissão de gasolina tem um diâmetro de 1,15m m e o reservatório de gasolina
A pressão no ponto S do sifão da figura não deve cair abaixo de 25k P a( a b s ) . Desprezando as perdas, determinar:A velocidade do fluido;A máxima altura do ponto S em relação ao ponto A ; p a t m =