Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Brunetti - Mecânica dos Fluidos - Ed: 2º - Capítulo 4.Exercício - Ex. 31
Na instalação da figura, todas as tubulações são de mesmo diâmetro (D = 138 mm); o registro é ajustado para que a vazão pela seção (1) seja a metade da vazão pela seção (2). Para tal condição, a altura manométrica da bomba vale 8 m e as perdas de carga valem, respectivamente:
Desprezando a perda de carga no ‘T’ na saída da bomba, determine sua potência, sendo seu rendimento 48%. ;.
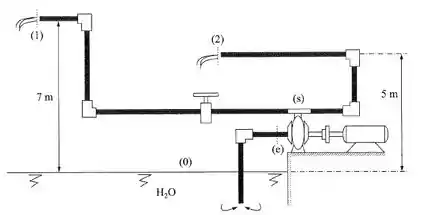
Passo 1
Conforme dito no enunciado, a vazão na seção 1 é metade da vazão em 2, ou seja:
Através do desenho, podemos ver que a vazão em 0 é a soma das vazões em 1 e 2, ou seja;
Dessa forma, como o diâmetro da tubulação é o mesmo, temos que:
E, pelo desenho, podemos ver também que:
Agora vamos calcular as cargas nos pontos 0, 1 e 2:
Passo 2
Agora vamos usar o princípio da conservação da energia para o sistema, assim, temos:
Agora vamos substituir os valores conhecidos na equação:
Simplificando a expressão (notando que os termos e aparecem em todos os termos) temos:
Passo 3
Agora vamos substituir as relações para as velocidades encontradas no passo 1 na última equação do passo 2, dessa forma, temos:
Simplificando a expressão, temos:
Agora, voltando as relações de velocidade encontradas no passo 1, substituindo esse valor na relação para :
Agora, calculando a vazão no ponto :
E, agora, calculando a potência real da bomba, temos: