Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 8.Problemas - Ex. 79
Explique o sistema de imagens necessário para simular o escoamento de uma fonte localizada assimetricamente entre duas paredes paralelas, como na Figura . Calcule a velocidade sobre a parede inferior em . Quantas imagens são necessárias para avaliar essa velocidade dentro de ?
Passo 1
E aí, tudo bem? Bora matar essa questão!
Vamos basicamente repetir o problema anterior, entretanto a distância vai mudar a partícula emissiva vai ter um par associado a distância equivalente, vamos adequar ao que o problema nos pede!
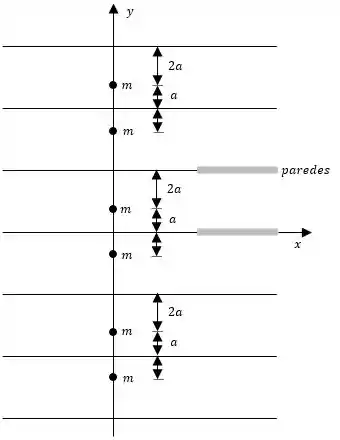
Como tivemos no problema anterior temos uma série básica para avaliar a velocidade, hehe:
Como a série se estende, o resultado almejado será obtido por volta do termo, onde:
Isso é tudo pessoal, conseguimos mais uma! \o/
Resposta
Após imagens!
Exercícios de Livros Relacionados
Considere o campo de velocidade pemanente, bidimensionaldado por V → =u ,v =1,3+2,8 x i →+1,5—2,8 y j → . Verifique se esse campo de escoamento é incompressível.
Imagine escoamento incompressível, permanente, bidimensional que é puramente circular no plano x y ou r θ . Em outras palavras, a componente de velocidade u θ é diferente de zero, mas u r é zero era t
Que restrições ou condições são impostas na função corrente Ψ de maneira que ela satisfaça exatamente a equação da continuidade bidimensional incompressível por definição? Porque essas restrições são
Considere o seguinte campo de velocidade permanente, tridimensional em coordenadas cartesianas: V →=( u ,v ,w )=a x y 2—b i →+c y 3 j →+d x y k → , onde a, b,c ,ed são constantes. Sob que condições es
Imagine escoamento incompressível, permanente, bidimensional que é puramente radial no plano x y ou r θ . Em outras palavras, a componente de velocidade u r é diferente de zero, mas u θ é zero era tod