Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 4.Problemas - Ex. 112
Estudantes estão brincando com uma mangueira de água. Quando eles a apontam para cima, o jato de água atinge apenas uma das janelas do escritório do Professor Pritchard, a 10 m de altura. Se o diâmetro da mangueira é de 1 cm, estime a vazão de água (L/min). O professor Pritchard desce e coloca sua mão um pouco acima da mangueira, obrigando o jato a sair pelos lados assimetricamente. Estime a pressão máxima e força total que ele sente. No dia seguinte, os estudantes estão brincando novamente; dessa vez, a meta é a janela do Professor Fox, 15 m acima. Ache a vazão (L/min) e a força total e a pressão máxima quando ele, naturalmente, aparece e bloqueia o escoamento.
Passo 1
Tá legal! Esse problema pode ser modelado como o problema 4.111, onde existe um fluxo de água na direção horizontal, e ao encontrar um anteparo, nesse caso, a mão dos professores, é defletida para ambos os lados, então, podemos aproveitar a ilustração do problema anterior e desenhar nosso volume de controle.
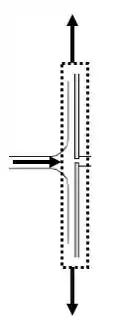
Então vamos começar analisando o problema para o primeiro caso, da janela do professor Pritchard, então, aplicando Bernoulli entre a saída do jato e a altura máxima atingida pela água:
Como os dois pontos de análise estão expostos ao ambiente, podemos cancelar os termos de pressão que aparecem, e sabendo que na altura máxima atingida pela água temos , a equação se torna:
E, com isso, podemos calcular a vazão de água nesse caso:
E, convertendo para
Passo 2
Agora, para calcular a pressão máxima pode ser encontrada através de Bernoulli entre a saída do jato e o ponto de contato em sua mão:
Como os dois pontos de análise estão expostos ao ambiente, podemos cancelar o termo de pressão do jato (que seria a pressão atmosférica) e calcular a pressão máxima relativa. E sabendo que quando o jato bate na mão do professor, podemos considerar esse ponto como sendo um ponto de estagnação, ou seja, , então a equação se torna:
Agora vamos aplicar a equação 4.18a apresentada nessa seção do equilíbrio de momento para o volume de controle do passo 1:
Como não temos força de campo na direção então e como o escoamento se dá em regime permanente, então a derivada no tempo também será zero, dessa forma, substituindo os valores conhecidos, temos:
E, nesse caso, temos , então, substituindo os valores conhecidos:
Então, a força total que o professor sente possui a mesma intensidade, mas sentido oposto, logo:
Passo 3
Agora vamos repetir os mesmos passos, só que para a mão e a janela do professor Fox, então, temos:
Como os dois pontos de análise estão expostos ao ambiente, podemos cancelar os termos de pressão que aparecem, e sabendo que na altura máxima atingida pela água temos , a equação se torna:
E, com isso, podemos calcular a vazão de água nesse caso:
E, convertendo para
Passo 4
Agora, para calcular a pressão máxima pode ser encontrada através de Bernoulli entre a saída do jato e o ponto de contato em sua mão:
Como os dois pontos de análise estão expostos ao ambiente, podemos cancelar o termo de pressão do jato (que seria a pressão atmosférica) e calcular a pressão máxima relativa. E sabendo que quando o jato bate na mão do professor, podemos considerar esse ponto como sendo um ponto de estagnação, ou seja, , então a equação se torna:
Agora vamos aplicar a equação 4.18a apresentada nessa seção do equilíbrio de momento para o volume de controle do passo 1:
Como não temos força de campo na direção então e como o escoamento se dá em regime permanente, então a derivada no tempo também será zero, dessa forma, substituindo os valores conhecidos, temos:
E, nesse caso, temos , então, substituindo os valores conhecidos:
Então, a força total que o professor sente possui a mesma intensidade, mas sentido oposto, logo: