Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 4.Problemas - Ex. 114

Um disco de 2 kg é restringido horizontalmente, mas está livre para mover na direção vertical. O disco é atingido por baixo por um jato vertical de água. Na saída do bocal, a velocidade e o diâmetro do jato de água são 10 m/s e 25 mm. Obtenha uma expressão geral para a velocidade do jato de água como uma função da altura, h . Determine a altura que o disco subirá e permanecerá estacionário.

Passo 1

Tá legal! Vamos começar esse exercício desenhando o volume de controle a ser utilizado:

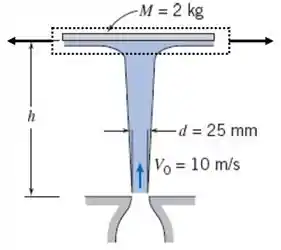
Agora vamos aplicar a equação de Bernoulli entre a saída do bocal e a placa onde a água escoa pelos lados, então temos:

p 0 ρ + v 0 2 2 + g ( 0 ) = p ρ + v 2 2 + g ( h )

Como os dois pontos de análise estão expostos ao ambiente, podemos cancelar os termos de pressão que aparecem, então, isolando a velocidade com que a água sai da placa, temos:

v = v 0 2 - 2 g h

Passo 2

Agora vamos aplicar a equação 4.18c apresentada nessa seção do equilíbrio de momento, para o volume de controle do passo 1:

F z = F S z + F B z = ∂ ∂ t ∫ V C   w ρ d V + ∫ S C   w ρ V → . d A →

Como o escoamento se dá em regime permanente, então a derivada no tempo será zero, dessa forma, substituindo os valores conhecidos, temos:

- M g = w 1 - ρ w 1 A 1

E, nesse caso, temos w 1 = v e A 1 = A , então, substituindo os valores conhecidos:

M g = ρ v 2 A

Passo 3

Agora, como da conservação de massa do sistema, a vazão que chega deve ser igual a vazão que sai, então:

ρ Q 0 = ρ Q → v 0 A 0 = v A

Substituindo a expressão encontrada para v A na última equação do passo 2, temos:

M g = ρ v 0 A 0 v

E, agora, substituindo o valor de v encontrado no passo 1:

M g = ρ v 0 A 0 v 0 2 - 2 g h → M g ρ v 0 A 0 = v 0 2 - 2 g h

Elevando ambos os lados ao quadrado, temos:

M g ρ v 0 A 0 2 = v 0 2 - 2 g h → h = 1 2 g v 0 2 - M g ρ v 0 A 0 2

Passo 4

Agora, substituindo os valores conhecidos na última equação do passo 3, temos:

h = 1 2 9,8 10 2 - 2 9,8 997 10 π 0,025 2 4 2 → h = 4,28   m

Resposta

v = v 0 2 - 2 g h

h = 4,28   m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

4.88 Uma cabeça cônica de jateamento é mostrada. O fluido é a água e a corrente de saída é uniforme. Avalie (a) a espessura do jato em forma de cortina de água no raio de 400 mm e (b) a força axial ex
4.91 Uma bomba a jato de água tem área do jato de 0,009 m² e velocidade do jato de 30,5 m/s. O jato está dentro de uma corrente secundária de água com velocidade V = 3m / s . A área total do duto (a s
4.90 Uma montagem com um bocal curvo que descarrega para a atmosfera é mostrada. A massa do bocal é 4,5 kg e seu volume interno é de 0,002 m³. O fluido é a água. Determine a força de reação exercida p
4.92 Um cotovelo redutor de 30° é mostrado. O fluido é água. Avalie as componentes da força que deve ser aplicada pelos tubos adjacentes para manter o cotovelo estático.
4.84 Um motor de foguete e combustível líquido consome, na condição de empuxo nominal, 80 kg/s de ácido nítrico como oxidante e 32 kg/s de anilina como combustível. Os gases de escape saem axialmente